Двоичные деревья поиска

Основные операции

Обычные деревья не дают выигрыша при хранении множества значений. При поиске элемента все равно необходимо просмотреть все дерево. Однако можно организовать хранение элементов в дереве так, чтобы при поиске элемента достаточно было просмотреть лишь часть дерева. Для этого надо ввести следующее требование упорядоченности дерева:

Двоичное дерево упорядочено, если для любой вершины x справедливо такое свойство: все элементы, хранимые в левом поддереве, меньше элемента, хранимого в x, а все элементы, хранимые в правом поддереве, больше элемента, хранимого в x.

Важное свойство упорядоченного дерева: все элементы его различны. Если в дереве встречаются одинаковые элементы, то такое дерево является частично упорядоченным.

В дальнейшем будет идти речь только о двоичных упорядоченных деревьях, слово «упорядоченный» будет опускаться.

Деревья поиска (search trees) позволяют выполнять следующие операции с дина-
мическими множествами: Search (поиск), Minimum (минимум), Maximum (мак-
симум), Predecessor (предыдущий), Successor (следующий), Insert (вста-
вить) и Delete (удалить). Таким образом, дерево поиска может быть исполь-
зовано и как словарь, и как очередь с приоритетами.

Время выполнения основных операций пропорционально высоте дерева. Если
двоичное дерево «плотно заполнено» (все его уровни имеют максимально возмож-
ное число вершин), то его высота (и тем самым время выполнения операций)
пропорциональна логарифму числа вершин. Напротив, если дерево представля-
ет собой линейную цепочку из n вершин, это время вырастает до .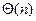

Конечно, возникающие на практике двоичные деревья поиска могут быть
далеки от случайных. Однако, приняв специальные меры по балансировке де-
ревьев, можно гарантировать, что высота дерева с n вершинами будет O (log n).

Реализация операций будет рассматриваться для двоичных деревьев, представленных как динамическая структура.

Реализацию этих операций приведем в виде соответствующих процедур.

Поиск

Алгоритм поиска можно записать в рекурсивном виде. Если искомое значение Item меньше Tree^.Data, то поиск продолжается в левом поддереве, если равен – поиск считается успешным, если больше – поиск продолжается в правом поддереве; поиск считается неудачным, если достигли пустого поддерева, а элемент найден не был.

function TreeSearch(Item: TypeElement; Tree: PTree): boolean;

{Поиск вершины дерева, содержащую значение Item}

var

Current: PTree;

begin

TreeSearch:= False;

if Tree <> nil then begin {Дерево не пустое}

Current:= Tree;

if Current^.Data = Item then {Вершина найдена}

TreeSearch:= True

else

if Current^.Data > Item then {Ищем в левом поддереве}

TreeSearch:= TreeSearch(Item, Current^.Left)

else {Ищем в правом поддереве}

TreeSearch:= TreeSearch(Item, Current^.Right);

end;

end;

Листинг 3.15 – Процедура поиска в двоичном дереве на языке Pascal

Листинг 3.24 – Рекурсивная процедура поиска в двоичном дереве поиска

Можно написать аналогичную нерекурсивную функцию. Она позволит избежать избыточного хранения информации. Каждый рекурсивный вызов размещает в стеке локальные переменные Item и Tree, а также адрес точки возврата из подпрограммы. В нерекурсивном варианте можно обойтись одной переменной Item и одной переменной Tree.

Листинг 3.25 – Нерекурсивная (итеративная) процедура поиска в двоичном дереве поиска

Минимум и максимум

Минимальный ключ в дереве поиска можно найти, пройдя по указателям left
от корня (пока не дойдем до NIL). Процедура возвращает указатель
на минимальный элемент поддерева с корнем х.

Листинг 3.26 – Процедура поиска минимального элемента в двоичном дереве поиска

Свойство упорядоченности гарантирует правильность процедуры

Tree-
Minimum. Если у вершины х нет левого ребёнка, то минимальный элемент
поддерева с корнем х есть х, так как любой ключ в правом поддереве не
меньше key [ x ]. Если же левое поддерево вершины х не пусто, то минимальный
элемент поддерева с корнем х находится в этом левом поддереве (поскольку
сам х и все элементы правого поддерева больше).

Алгоритм Tree-Maximum симметричен:

Листинг 3.27 – Процедура поиска максимального элемента в двоичном дереве поиска

Оба алгоритма требуют времени O (h), где h — высота дерева (поскольку двигаются по дереву только вниз).

Следующий и предыдущий элементы

Как найти в двоичном дереве элемент, следующий за данным? Свойство
упорядоченности позволяет сделать это, двигаясь по дереву. Вот процедура,
которая возвращает указатель на следующий за х элемент (если все ключи
различны, он содержит следующий по величине ключ) или NIL, если элемент -
последний в дереве:

Листинг 3.28 – Процедура поиска следующего (в смысле порядка на ключах) элемента в двоичном дереве поиска

Процедура Tree-Successor отдельно рассматривает два случая. Если пра-
вое поддерево вершины х непусто, то следующий за х элемент минимальный элемент в этом поддереве и равен Tree-Minimum(right [ x ]).

Пусть теперь правое поддерево вершины х пусто. Тогда мы идём от х вверх,
пока не найдём вершину, являющуюся левым сыном своего родителя (строки
3 – 7). Этот родитель (если он есть) и будет искомым элементом. Формально
говоря, цикл в строках 4 – 6 сохраняет такое свойство: у = p [ z ]; искомый элемент
непосредственно следует за элементами поддерева с корнем в х.

Время работы процедуры Tree-Successor на дереве высоты h есть O (h),
так как мы двигаемся либо только вверх, либо только вниз.

Процедура Tree-Predecessor симметрична. Таким образом, мы доказали следующую теорему.

Теорема. Операции Search, Minimum, Maximum, Successor и Predecessor на дереве высоты h выполняются за время O (h).

Добавление и удаление

Далее будет рассмотрен нерекурсивный алгоритм добавления элемента в дерево. Сначала надо найти вершину, к которой в качестве потомка необходимо добавить новую вершину (фактически, произвести поиск), а затем присоединить к найденной новую вершину, содержащую значение Item (процедура написана в предположении, что добавляемого элемента в дереве нет).

procedure TreeAdd(Item: TypeElement; var Tree: PTree);

{Добавление в дерево вершины со значением Item}

var

NewNode, Current: PTree;

begin

if Tree = nil then begin {Дерево пустое}

{Создаем корень}

New(Tree);

Tree^.Data:= Item;

Tree^.Left:= nil;

Tree^.Right:= nil;

end else begin

Current:= Tree;

{Поиск вершины}

while ((Item > Current^.Data) and (Current^.Right <> nil)) or

((Item < Current^.Data) and (Current^.Left <> nil)) do

if Item > Current^.Data then

Current:= Current^.Right

else

Current:= Current^.Left;

{Создание новой вершины}

New(NewNode);

NewNode^.Data:= Item;

NewNode^.Left:= nil;

NewNode^.Right:= nil;

If Item > Current^.Data then {Новая вершина больше найденной}

Current^.Right:= NewNode {Присоединяем новую справа}

else {Новая вершина меньше найденной}

Current^.Left:= NewNode; {Присоединяем новую слева}

end;

end;

Листинг 3.29 – Процедура добавления элемента в двоичное дерево поиска

Листинг 3.30 – Процедура добавления элемента в двоичное дерево поиска

Процедура удаления элемента будет несколько сложнее. При удалении может случиться, что удаляемый элемент находится не в листе, то есть вершина имеет ссылки на реально существующие поддеревья. Эти поддеревья терять нельзя, а присоединить два поддерева на одно освободившееся после удаления место невозможно. Поэтому необходимо поместить на освободившееся место либо самый правый элемент из левого поддерева, либо самый левый из правого поддерева. Нетрудно убедиться, что упорядоченность дерева при этом не нарушится. Договоримся, что будем заменять самый левый элемент из правого поддерева (следующий в смысле порядка на ключах, Successor).

Нельзя забывать, что при замене вершина, на которую производится замена, может иметь правое поддерево. Это поддерево необходимо поставить вместо перемещаемой вершины.

procedure TreeDelete(Item: TypeElement; var Tree: PTree);

{Удаление из дерева вершины со значением Item}

var

Parent, Cur, Cur2: PTree;

Direction: (L, R); {направление движения (влево/вправо)}

begin

{Поиск удаляемого элемента}

Parent:= nil; {предок удаляемой вершины}

Cur:= Tree;

while ((Item > Cur^.Data) and (Cur^.Right <> nil)) or

((Item < Cur^.Data) and (Cur^.Left <> nil)) do begin

Parent:= Cur;

if Item > Cur^.Data then begin

Cur:= Cur^.Right; Direction:= R;

end else begin

Cur:= Cur^.Left; Direction:= L;

end;

end;

if Cur <> nil then begin {Вершина найдена}

{Анализируем наличие потомков у найденной вершины}

{и удаляем соответствующим образом}

if (Cur^.Left <> nil) and (Cur^.Right <> nil) then begin

{Удаление вершины в случае наличия у нее обоих потомков}

Parent:= Cur; Cur2:= Cur^.Right;

{Поиск кандидатуры на замену}

while Cur2^.Left <> nil do begin

Parent:= Cur2; Cur2:= Cur2^.Left;

end;

{Заменяем}

Cur^.Data:= Cur2^.Data;

{Спасаем правое поддерево вершины, которой заменяем}

if Parent <> Cur then

Parent^.Left:= Cur2^.Right

else

Parent^.Right:= Cur2^.Right;

Dispose(Cur2);

end else begin

{Удаление вершины в случае наличия у нее}

{не более одного потомка}

if (Cur^.Left = nil) then begin

if Parent <> nil then begin

if Direction = L then

Parent^.Left:= Cur^.Right

else

Parent^.Right:= Cur^.Right;

end else begin

Tree:= Cur^.Right;

end;

end;

if (Cur^.Right = nil) then begin

if Parent <> nil then begin

if Direction = L then

Parent^.Left:= Cur^.Left

else

Parent^.Right:= Cur^.Left;

end else begin

Tree:= Cur^.Left;

end;

end;

Dispose(Cur);

end;

end;

end;

Листинг 3.31 – Процедура удаления элемента из двоичного дерева поиска

Листинг 3.32 – Процедура удаления элемента из двоичного дерева поиска

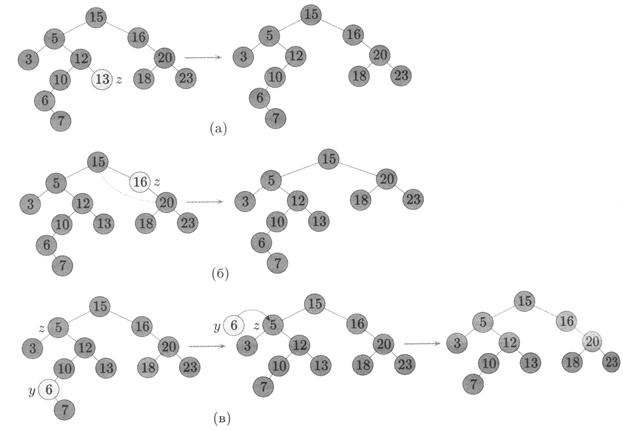
Рисунок 3.14 – Удаление элемента из двоичного дерева поиска

Удаление вершины z из двоичного дерева поиска. (а) Если вершина z не имеет детей её можно удалить без проблем. (6) Если вершина z имеет одного ребёнка, помещаем его на место вершины z. (в) Если у вершины z двое детей, процесс сводится
к предыдущему случаю, т.е. удаляем вместо неё вершину у с непосредственно следующим
значением ключа (у этой вершины ребёнок один) и помещая ключ kеу [ у ] (и связанные с ним
дополнительные данные) на место вершины z.

Временная сложность этих алгоритмов (она одинакова для этих алгоритмов, так как в их основе лежит поиск) оценим для наилучшего и наихудшего случая. В лучшем случае, – то есть случае полного двоичного дерева – получаем сложность O _min (log n). В худшем случае дерево может выродиться в список. Такое может произойти, например, при добавлении элементов в порядке возрастания. При работе со списком в среднем придется просмотреть половину списка. Это даст сложность O _max (n).

В процедуре очистки дерева применяется обратный метод обхода дерева. Использование обратного метода обхода гарантирует, что будут сначала посещены и удалены все потомки предка, прежде чем удалится сам предок.

procedure TreeClear(var Tree: PTree);

{Очистка дерева}

begin

if Tree <> nil then begin

TreeClear(Tree^.Left);

TreeClear(Tree^.Right);

Dispose(Tree);

Tree:= nil;

end;

end;

Листинг 3.33 – Процедура очистки двоичного дерева поиска

Временная сложность этой операции O (n).

Случайные деревья поиска

Случайные деревья поиска представляют собой упорядоченные бинарные деревья поиска, при создании которых элементы (их ключи) вставляются в случайном порядке.

При создании таких деревьев используется тот же алгоритм, что и при добавлении вершины в бинарное дерево поиска. Будет ли созданное дерево случайным или нет, зависит от того, в каком порядке поступают элементы для добавления. Примеры различных деревьев, создаваемых при различном порядке поступления элементов приведены ниже.

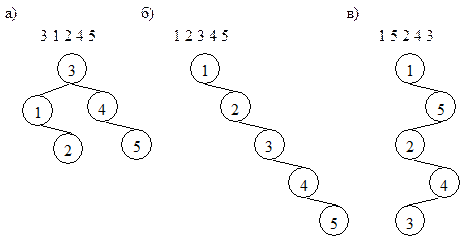
Рисунок 3.15 – Случайные и вырожденные деревья поиска

При поступлении элементов в случайном порядке получаем дерево с минимальной высотой h (см. рис. 3.12.а), а соответственно минимизируется время поиска элемента в таком дереве, которое пропорционально O (log n). При поступлении элементов в упорядоченном виде (см. рис. 3.12.б) или в несколько необычном порядке (см. рис. 3.12.в) происходит построение вырожденных деревьев поиска (оно вырождено в линейный список), что нисколько не сокращает время поиска, которое составляет O (n).

Оптимальные деревья поиска

При поиске в двоичном дереве одни элементы могут искаться чаще, чем другие, то есть существуют вероятности p_k поиска k -го элемента и для различных элементов эти вероятности неодинаковы. Можно сразу предположить, что поиск в дереве в среднем будет более быстрым, если те элементы, которые ищутся чаще, будут находиться ближе к корню дерева.

Пусть даны 2× n + 1 вероятностей p ₁, p ₂, …, p_n, q ₀, q ₁, …, q_n, где

p_i – вероятность того, что аргументом поиска является K_i;

q_i – вероятность того, что аргумент поиска лежит между K_i и K_{i +1};

q ₀ – вероятность того, что аргумент поиска меньше, чем K ₁;

q_n – вероятность того, что аргумент поиска больше, чем K_n;

Тогда цена дерева поиска C будет определяться следующим образом:

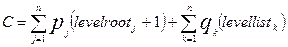
где levelroot_j – уровень узла j, а levellist_k – уровень листа k.

Дерево поиска называется оптимальным, если его цена минимальна или, другими словами, оптимальное бинарное дерево поиска – это бинарное дерево поиска, построенное в расчете на обеспечение максимальной производительности при заданном распределении вероятностей поиска требуемых данных.

Существует подход построения оптимальных деревьев поиска, при котором элементы вставляются в порядке уменьшения частот, что дает в среднем неплохие деревья поиска. Однако этот подход может дать вырожденное дерево поиска, которое будет далеко от оптимального.

Еще один подход состоит в выборе корня k таким образом, чтобы максимальная сумма вероятностей для вершин левого поддерева или правого поддерева была настолько мала, насколько это возможно. Такой подход также может оказаться плохим в случае выбора в качестве корня элемента с малым значением p_k.

Существуют алгоритмы, которые позволяют построить оптимальное дерево поиска. К ним относится, например, алгоритм Гарсия-Воча. Однако такие алгоритмы имеют временную сложность порядка O (n ²), а некоторые еще имеют такую же пространственную сложность. Таким образом, создание оптимальных деревьев поиска требует больших накладных затрат, что не всегда оправдывает выигрыш при быстром поиске.