Основные принципы разработки алгоритмов

Прямая адресация; таблицы с прямой адресацией

Прямая адресация применима, если количество возможных ключей невелико. Пусть возможными ключами являются числа из множества U = {0,1,...,m – 1} (число т не очень велико). Предположим также, что ключи всех элементов различны.

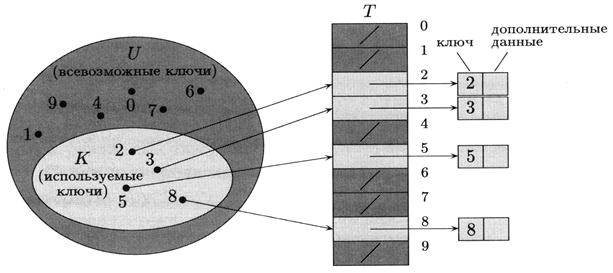
Рисунок 4.2 – Реализация динамического множества с помощью таблицы с прямой адресацией

Для хранения множества используется массив Т [0.. т – 1], называемый таблицей с прямой адресацией (direct-address table). Каждая позиция,или ячей­ка,(position, slot) соответствует определённому ключу из множества U.

T [ k ] – место, предназначенное для записи указателя на элемент с ключом k; если элемента с ключом k в таблице нет, то T [ k ] = NIL). Реализация словарных операций тривиальна:

Листинг 4.1 – Словарные операции при прямой адресации

Каждая из этих операций требует времени O (1).

Иногда можно сэкономить место, записывая в таблицу Т не указатели на элементы множества, а сами эти элементы. Можно обойтись и без отдельного поля «ключ»: ключом служит индекс в массиве. Впрочем, если мы обходимся без ключей и указателей, то надо иметь способ указать, что данная позиция свободна.

4.3 Хеш – таблицы; возникновение коллизий и их разрешение

Прямая адресация обладает очевидным недостатком: если множество U все­возможных ключей велико, то хранить в памяти массив Т размером ‌ U ‌ непрак­тично, а то и невозможно. Кроме того, если число реально присутствующих е таблице записей мало по сравнению с | U |, то много памяти тратится зря.

Если количество записей в таблице существенно меньше, чем количество все­возможных ключей, то хеш-таблица занимает гораздо меньше места, чем табли­ца с прямой адресацией. Именно, хеш-таблица требует памяти объёмом Θ(| К |) где К – множество записей, при этом время поиска в хеш-таблице по-прежнему есть О (1) (единственное «но» в том, что на сей раз это – оценка в среднем, ане в худшем случае, да и то только при определённых предположениях).

В то время как при прямой адресации элементу с ключом k отводится пози­ция номер k, при хешировании этот элемент записывается в позицию номер h (k)в хеш-таблице (hash table) T [0.. m – 1], где

h: U→ {0, l,..., m – l}

– некоторая функция, называемая хеш-функцией (hash function). Число h (k)называют хеш-значением (hash value) ключа k. Использование массива длины т, а не | U|,дает экономию памяти.

Однако, проблема заключается в том, что хеш-значения двух разных ключей могут совпасть. В таких случаях говорят, что случилась коллизия,или столкновение (collision). К счастью, эта проблема разрешима: хеш-функциями можно пользоваться и при наличии столкновений.

Хотелось бы выбрать хеш-функцию так, чтобы коллизии были невозможны. Но при | U| > т неизбежно существуют разные ключи, имеющие одно и то же хеш-значение. Так что можно лишь надеяться, что для фактически присутствующих в множестве ключей коллизий будет немного, и быть готовыми обрабатывать те коллизии, которые всё-таки произойдут.

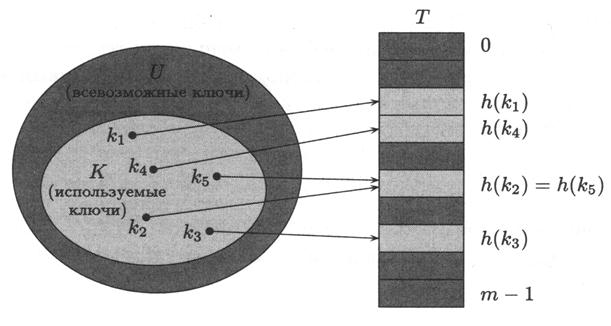
Рисунок 4.3 – Использование хеш-функции для отображения ключей в позиции хеш-таблицы (хеш-значения ключей k₂ и k₅ совпадают – имеет место коллизия)

При выборе хеш-функции обычно не известно, какие именно ключи будут храниться. Но на всякий случай разумно сделать хеш-функцию в каком-то смысле «случайной», хорошо перемешивающей ключи по ячейкам (английский глагол " to hash " означает «мелко порубить, помешивая»). Разумеется, «случайная» хеш-функция должна всё же быть детерминированной в том смысле, что при ее повторных вызовах с одним и тем же аргументом она должна возвращать одно и то же хеш-значение.

В этом разделе будет рассмотрен простейший способ обработки (как говорят, «разрешения») коллизий с помощью цепочек (другим способом разрешения коллизий является открытая адресация, он будет рассмотрен в следующем подразделе).

Разрешение коллизий с помощью цепочек

Технология сцепления элементов (chaining) состоит в том, что элемент множества, которым соответствует одно и то же хеш-значение, связывают в цепочку-список. В позиции номер j хранится указатель на голову списка тех элементов, у которых хеш-значение ключа равно j если таких элементов в множестве нет, в позиции j записан NIL. Операции добавления, поиска и удаления реализуются легко:

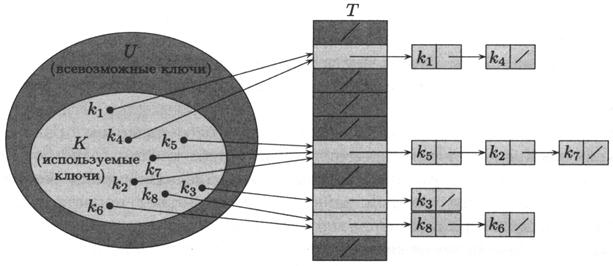
Рисунок 4.4 – Использование цепочек для разрешения коллизий

Листинг 4.2 – Словарные операции при хешировании с цепочками

Рассмотрим алгоритмы основных операций с хеш-таблицей, при открытом хешировании. В этих алгоритмах будем использовать структуры данных и операции с линейными однонаправленными списками. Поле Data в элементах списка будет здесь исполнять роль ключа, а роль указателя на список ptrHead будет играть элемент хеш-таблицы.

const

В = {подходящая константа};

type

ChainedHashTable = array[0..B-1] of PElement;

Кроме того, здесь используется предопределенная функция h (x), которая и является собственно реализацией хеш-функции.

procedure Clear_ChainedHashTable (var A: ChainedHashTable);

{Процедура очистки хеш-таблицы}

var

IndexSeg: integer;

begin

for IndexSeg:=0 to B-1 do

while A[IndexSeg] <> nil do

Del_LineSingleList(A[IndexSeg], A[IndexSeg]);

end;

function Find_ChainedHashTable(x: TypeData;

var A: ChainedHashTable;

var current: PElement): boolean;

{функция поиска элемента x в хеш-таблице. Принимает значение true, если найден и возвращает указатель, который устанавливается на найденный элемент, или принимает значение false и возвращает nil}

var

IndexSeg: integer; {номер сегмента}

begin

IndexSeg:= h(x);

{начало списка, в котором надо искать, это A[IndexSeg]}

if Find_LineSingleList(x, A[IndexSeg], current) then

Find_ChainedHashTable:= true

else

Find_ChainedHashTable:= false;

end;

procedure Add_ChainedHashTable(x: TypeData; var A: ChainedHashTable);

{Процедура добавления элемента x в хеш-таблицу}

var

IndexSeg: integer; {номер сегмента}

current: PElement;

begin

if not Find_ChainedHashTable(x, A, current) then begin

{Если в таблице элемент уже есть, то добавлять не надо}

IndexSeg:= h(x);

{Добавляем всегда в начало списка}

InsFirst_LineSingleList(x, A[IndexSeg]);

end

end;

procedure Del_ChainedHashTable(x: TypeData; var A: ChainedHashTable);

{Процедура удаления элемента x из хеш-таблицы}

var

IndexSeg: integer; {номер сегмента}

current: PElement;

begin

if Find_ChainedHashTable(x, A, current) then begin

{Если в таблице элемент еще есть, то удаляем}

IndexSeg:= h(x);

Del_LineSingleList(A[IndexSeg], current);

end

end;

Листинг 4.3 – Словарные операции при хешировании с цепочками

Операция добавления работает в худшем случае за время О (1). Максималь­ное время работы операции поиска пропорционально длине списка (ниже мы рассмотрим этот вопрос подробнее). Наконец, удаление элемента можно прове­сти за время О (1) – при условии, что списки двусторонне связаны (если списки связаны односторонне, то для удаления элемента х надо предварительно найти его предшественника, для чего необходим поиск по списку; в таком случае стоимость удаления и поиска примерно одинаковы).

Анализ хеширования с цепочками

Пусть Т – хеш-таблица с т позициями, в которую занесено п элементов. Коэффициентом заполнения (load factor) таблицы называется число α = n/m (это число может быть и меньше, и больше единицы). Далее стоимость операций будет оцениваться в терминах α.

В худшем случае хеширование с цепочками неоптимально: если хеш-значения всех n ключей совпадают, то таблица сводится к одному списку длины n, и на поиск будет тратиться то же время Θ(n), что и на поиск списке, плюс ещё время на вычисление хеш-функции. Конечно, в такой ситуации хеширование бессмысленно.

Средняя стоимость поиска зависит от того, насколько равномерно хеш-функция распределяет хеш-значения по позициям таблицы. Будем условно предполагать, что каждый данный элемент может попасть в любую из m позиций таблицы с равной вероятностью и независимо от того, куда попал другой элемент. Это предположение называется гипотезой «равномерного хеширования» (simple uniform hashing).

Положим также, что для данного ключа k вычисление хеш-значения h (k)шаг по списку и сравнение ключей требует фиксированного времени, так что время поиска элемента с ключом k линейно зависит от количества элементов списке T [ h (k)], которые мы просматриваем в процессе поиска. Будем различать два случая: в первом случае поиск оканчивается неудачей (элемента с ключом в списке нет), во втором поиск успешен – элемент с требуемым ключом обнаруживается.

Теорема 4.1. Пусть Т – хеш-таблица с цепочками, имеющая коэффициент заполнения α. Предположим, что хеширование равномерно. Тогда при поиске элемента, отсутствующего в таблице, будет просмотрено в среднем α элементов таблицы, а среднее время такого поиска (включая время на вычисление хеш-функции) будет равно Θ(1 + α).

Доказательство. Поскольку в предположении равномерного хеширования все позиции таблицы для данного ключа равновероятны, среднее время поиска отсутствующего элемента совпадает со средним временем полного просмотра одного из т списков, то есть пропорционально средней длине наших m списков. Эта средняя длина есть п/т = α, откуда получаем первое утверждение теоремы; второе утверждение получится, если добавить время Θ(1) на вычисление хеш-значения.

Теорема 4.2. При равномерном хешировании среднее время успешного поиска в хеш-таблице с цепочками есть Θ(1 + α), где α – коэффициент заполнения.

Доказательство. Хотя формулировка этой теоремы похожа на предыдущую, смысл утверждения несколько иной. В предыдущей теореме рассматривалась произвольная таблица с коэффициентом заполнения α и оценивалось среднее число действий, необходимых для поиска случайного элемента, равновероятно попадающего во все ячейки таблицы. В этой теореме так делать нельзя: если мы возьмём произвольную таблицу и, считая все её элементы равновероятными, будем искать среднее время поиска случайно выбранного из них, то оценки вида Θ(1 + α) не получится (контрпример: таблица, в которой все элементы попали в один список).

Формулировка подразумевает двойное усреднение: сначала мы рассматрива­ем случайно выбранную последовательность элементов, добавляемых в таблицу причём на каждом шаге все значения ключа равновероятны и шаги независи­мы, а затем в полученной таблице выбираем элемент для поиска, считая все её элементы равновероятными.

Посмотрим на ситуацию в тот момент, когда таблица уже построена, не случайный элемент для поиска ещё не выбран. Чему равно среднее время по­иска, усреднённое по всем п элементам таблицы? Надо сложить позиции всех элементов в своих списках и поделить сумму на п (общее число элементов).

Если представить себе, что при заполнении таблицы элементы дописывались в конец соответствующих списков, то упомянутая сумма по порядку величины равна общему число операций, выполненных при заполнение таблицы (поскольку при добавлении в конец и при поиске выполняется одно и то же количество действий).

Теперь вспомним об усреднении по различным возможностям в процессе построения таблицы. При добавлении в неё i -го элемента математическое ожи­дание числа действий равно Θ(1 + (i – 1) / m) (см. доказательство предыдущей теоремы), и потому математическое ожидание общего числа действий при за­полнении таблицы, делённое на n, есть

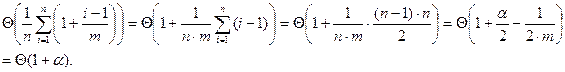
Если количество позиций в хеш-таблице считать пропорциональным числу элементов в таблице, то из доказанных теорем вытекает, что среднее время на поиск (в оптимистических предположениях о распределении вероятностей) есть O (1). В самом деле, если n = O (m), то α = п / т = O (1) и O (1 + α) = O (1). Поскольку стоимость добавления в хеш-таблицу с цепочками есть О (1), а стоимость удаления элемента есть O (1) (мы считаем, что списки двусторонне связаны), среднее время выполнение любой словарной операции (в предположении равномерного хеширования) есть O (1).

4.4 Способы построения хеш – функций

Выбор хорошей хеш-функции

Хорошая хеш-функция должна (приближенно) удовлетворять предположениям равномерного хеширования: для очередного ключа все т хеш-значений должны быть равновероятны. Чтобы это предположение имело смысл, фиксируем распределение вероятностей Р на множестве U; будем предполагать, что ключи выбираются из U независимо друг от друга, и каждый распределён в соответствии с Р. Тогда равномерное хеширование означает, что

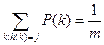для j=0,1,…,m – 1(4.1)

К сожалению, распределение Р обычно неизвестно, так что проверить это не­возможно (да и ключи не всегда разумно считать независимыми).

Изредка распределение Р бывает известно. Пусть, например, ключи – слу­чайные действительные числа, независимо и равномерно распределённые на про­межутке [0,1). В этом случае легко видеть, что хеш-функция h (k) = ë km ûудо­влетворяет условию (4.1).

На практике при выборе хеш-функций пользуются различными эвристи­ками, основанными на специфике задачи. Например, компилятор языка про­граммирования хранит таблицу символов, в которой ключами являются иден­тификаторы программы. Часто в программе используется несколько похожих идентификаторов (например, «pt» и «pts»). Хорошая хеш-функция будет стараться, чтобы хеш-значения у таких похожих идентификаторов были различны.

Обычно стараются подобрать хеш-функцию таким образом, чтобы её пове­дение не коррелировало с различными закономерностями, которые могут встре­титься в хешируемых данных. Например, описываемый ниже метод деления с остатком состоит в том, что в качестве хеш-значения берётся остаток от деления ключа на некоторое простое число. Если это простое число никак не связано с функцией распределения Р, то такой метод даёт хорошие результаты.

Заметим в заключение, что иногда желательно, чтобы хеш-функция удо­влетворяла условиям, выходящим за пределы требования равномерного хеши­рования. Например, можно стараться, чтобы «близким» в каком-либо смысле ключам соответствовали «далёкие» хеш-значения (это особенно желательно при использовании описанной в разделе 4.5 линейной последовательности проб).

Ключи как натуральные числа

Обычно предполагают, что область определения хеш-функции – множество целых неотрицательных чисел. Если ключи не являются натуральными числами, их обычно можно преобразовать к такому виду (хотя числа могут получиться большими). Например, последовательности символов можно интерпретировать как числа, записанные в системе счисления с подходящим основанием: иденти­фикатор «pt» – это пара чисел (112,116) (таковы ASCII-коды букв «р» и «t»), или же число (112×128) + 116 = 14452 (в системе счисления по основанию 128). Далее мы всегда будем считать, что ключи – целые неотрицательные числа.

Деление с остатком

Построение хеш-функции методом деления с остатком (division method) состоит в том, что ключу k ставится в соответствие остаток от деления k на m, где т – число возможных хеш-значений:

h (k) – k mod m.

Например, если размер хеш-таблицы равен m = 12 и ключ равен 100, то хеш-значение равно 4.

При этом некоторых значений m стоит избегать. Например, если m = 2^Р, то h (k) –это просто р младших битов числа k. Если нет уверенности, что все комбинации младших битов ключа будут встречаться с одинаковой частотой, то степень двойки в качестве числа т не выбирают. Нехорошо также выбирать в качестве т степень десятки, если ключи естественно возникают как десятич­ные числа: ведь в этом случае окажется, что уже часть цифр ключа полностью определяет хеш-значение. Если ключи естественно возникают как числа в си­стеме счисления с основанием 2^Р, то нехорошо брать m = 2 ^Р – 1, поскольку при этом одинаковое хеш-значение имеют ключи, отличающиеся лишь перестановкой «2^р-ичных цифр».

Хорошие результаты обычно получаются, если выбрать в качестве m про­стое число, далеко отстоящее от степеней двойки. Пусть, например, нам надо поместить примерно 2000 записей в хеш-таблицу с цепочками, причем нас не пугает возможный перебор трёх вариантов при поиске отсутствующего в таб­лице элемента. Что ж, воспользуемся методом деления с остатком при длине хеш-таблицы m = 701. Число 701 простое, 701 ~ 2000/3, и до степеней двойки от числа 701 тоже далеко. Стало быть, можно выбрать хеш-функцию вида

h (k) = k mod 701.

На всякий случай можно ещё поэкспериментировать с реальными данными на предмет того, насколько равномерно будут распределены их хеш-значения.

Умножение

Построение хеш-функции методом умножения (multiplication method) состо­ит в следующем. Пусть количество хеш-значений равно т. Зафиксируем кон­станту А в интервале 0 < А < 1, и положим

h (k) = ë m (k A mod 1)û,

где k×A mod 1 – дробная часть k×A.

Достоинство метода умножения в том, что качество хеш-функции мало зависит от выбора m. Обычно в качестве т выбирают степень двойки, поскольку в большинстве компьютеров умножение на такое т реализуется как сдвиг слова. Пусть, например, длина слова в нашем компьютере равна w битам и ключ k помещается в одно слово. Тогда, если т = 2 ^Р, то вычисление хеш-функции можно провести так: умножим k на m -битовое целое число А× 2 ^w (предполагается, что это число является целым); получится 2 w -битовое число. Пусть r₀ – число, образованное младшими w разрядами; старшие р битов в r₀ образуют искомое хеш-значение (рис. 4.5).

Метод умножения работает при любом выборе константы А, но некоторые значения А могут быть лучше других. Оптимальный выбор зависит от того, какого рода данные подвергаются хешированию.

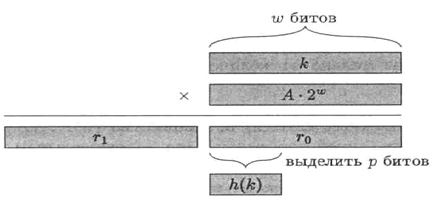
Рисунок 4.5 – Хеширование с использованием умножения

В одной своей книге Кнут обсуждает выбор константы А и приходит к выводу, что значение

A»(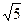– 1)/2 = 0,6180339887…

является довольно удачным (золотое сечение).

Универсальное хеширование

Если недоброжелатель будет специально подбирать данные для хеширова­ния, то (зная функцию h)он может устроить так, что все п ключей будут соответствовать одной позиции в таблице, в результате чего время поиска будет равно Q(n). Любая фиксированная хеш-функция может быть дискредитирована таким образом. Единственный выход из положения – выбирать хеш-функцию случайным образом, не зависящим от того, какие именно данные вы хешируете. Такой подход называется универсальным хешированием (universal hashing). Что бы ни предпринимал ваш недоброжелатель, если он не имеет информации о выбранной хеш-функции, среднее время поиска останется хорошим.

Основная идея универсального хеширования – выбирать хеш-функцию во время исполнения программы случайным образом из некоторого множества. Стало быть, при повторном вызове с теми же входными данными алгоритм будет работать уже по-другому. Как и в случае с алгоритмом быстрой сор­тировки, рандомизация гарантирует, что нельзя придумать входных данных, на которых алгоритм всегда бы работал медленно (в примере с компилято­ром и таблицей символов не сможет получиться, что какой-то определённый стиль выбора идентификаторов приводит к замедлению компиляции: вероятность, что компиляция замедлится из-за неудачного хеширования, во-первых мала, и во-вторых, зависит только от количества идентификаторов, но не от их выбора).

Пусть Н – конечное семейство функций, отображающих данное множество U (множество всевозможных ключей) во множество (0,1,..., m – 1} (множество хеш-значений). Это семейство называется универсальным (universal), если для любых двух ключей х,у Î U число функций h Î H, для которых h (x) = h (y), равно |H | / т. Иными словами, при случайном выборе хеш-функции вероятность коллизии между двумя данными ключами должна равняться вероятности совпадения двух случайно выбранных хеш-значений (которая равна 1 / m).

Следующая теорема показывает, что универсальное семейство хеш-функций обеспечивает хорошую производительность в среднем.

Теорема 4.3. Пусть нам необходимо поместить n фиксированных ключей в таблицу размера m, где m ³ n, и хеш-функция выбирается случайным образом из универсального семейства. Тогда математическое ожидание числа коллизий, в которых участвует данный ключ х, меньше единицы.

Доказательство. Математическое ожидание числа коллизий данного ключа с данным ключом у равно 1 / m по определению универсального семейства, поскольку всего имеется n – 1 ключей, отличных от х, математическое ожидание числа коллизий с каким-нибудь из этих ключей равно (п – 1) / m, что меньше единицы, поскольку n £ m.

Как же построить универсальное семейство? Нам поможет в этом элементарная теория чисел. Число m (количество хеш-значений) выберем простым. Будем считать, что каждый ключ представляет собой последовательность r + 1 «байтов» (байт, или символ, – это просто двоичное число с ограниченным числом разрядов; мы будем считать, что максимальное значение байта меньше r. Для каждой последовательности а = á a₀,a₁,...,а_г ñ, элементы которой являются вычетами по модулю m (то есть принадлежат множеству {0,1,..., m – 1} - рассмотрим функцию h_a, заданную формулой

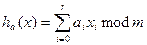(4.2)

где ключ х есть последовательность байтов á x₀, x₁,...,x _rñ. Положим

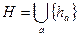(4.3)

Очевидно, множество H содержит m^r+1 элементов.

Теорема 4.4. Семейство функций H, определённое формулами (4.2) и (4.3) является универсальным семейством хеш-функций.

Доказательство. Пусть х = á х ₀ ,х ₁ ,…,х _rñи у = á у ₀ ,y ₁ ,...,y _rñ – два различных ключа;

не ограничивая общности, можно считать, что x ₀ ≠ y ₀. Если а = áа₀, a₁,...,а_гñ, то h_a (x)= h_a (y)тогда и только тогда, когда

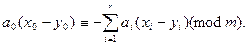
Поскольку x ₀ – y ₀ ≠ 0 (mod m), для каждой последовательности áа₁,..., а_r ñсуществует

и единственно значение а ₀, при котором это равенство выполнено. Количество таких последовательностей равно т^r, и таково же, стало быть, количество функций из H, не различающих ключи х и у. Поскольку т^r = |Н| / т, всё доказано.

Справедливой будет следующая интерпретация: ненулевой линейный функционал h → h (x – у)с равной вероятностью принимает любое из т своих значений, в том числе 0.

4.5 Открытая адресация; способы вычисления последовательности испробованных мест: линейная последовательность проб, квадратичная последовательность проб, двойное хеширование

В отличие от хеширования с цепочками, при открытой адресации (open addressing) никаких списков нет, а все записи хранятся в самой хеш-таблице каждая ячейка таблицы содержит либо элемент динамического множества, либо NIL. Поиск заключается в том, что мы определённым образом просматриваем элементы таблицы, пока не найдём то, что ищем, или не удостоверимся, что элемента с таким ключом в таблице нет. Тем самым число хранимых элементов не может быть больше размера таблицы: коэффициент заполнения не больше 1.

Конечно, и при хешировании с цепочками можно использовать свободные места в хеш-таблице для хранения списков, но при открытой адресации указатели вообще не используются: последовательность просматриваемых ячеек вычисляется. За счет экономии памяти на указателях можно увеличить количество позиций в таблице, что уменьшает число коллизий и сокращает поиск.

Чтобы добавить новый элемент в таблицу с открытой адресацией, ячейки которой занумерованы целыми числами от 0 до т – 1, мы просматриваем её, пока не найдем свободное место. Если всякий раз просматривать ячейки подряд (от 0-й до (m – 1)-й), потребуется время Q(n), но суть в том, что порядок просмотра таблицы зависит от ключа. Иными словами, мы добавляем к хеш-функции второй аргумент – номер попытки (нумерацию начинаем с нуля), так что хеш-функция имеет вид

h: U x {0,1,..., m – 1} → {0, 1,..., m – 1}

(U – множество ключей). Последовательность испробованных мест, или последовательность проб(probe sequence), для данного ключа k имеет вид

h (k, 0) ,h (k, 1) ,…,h (k,m – 1);

функция h должна быть такой, чтобы каждое из чисел от 0 до т – 1 встретилось в этой последовательности ровно один раз (для каждого ключа все позиции таблицы должны быть доступны). Ниже приводится текст процедуры добавления в таблицу Т соткрытой адресацией; в нем подразумевается, что записи не содержат дополнительной информации, кроме ключа. Если ячейка таблицы пуста, в ней записан NIL (фиксированное значение, отличное от всех ключей).

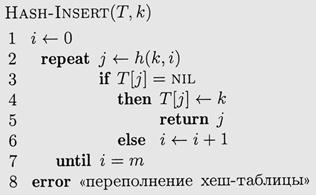
Листинг 4.4 – Процедура добавления элемента в таблицу с открытой адресацией

При поиске элемента с ключом k в таблице с открытой адресацией ячей­ки таблицы просматриваются в том же порядке, что и при добавлении в нее элемента с ключом k. Если при этом мы натыкаемся на ячейку, в которой записан NIL, то можно быть уверенным, что искомого элемента в таблице нет (иначе он был бы занесён в эту ячейку). (Внимание: предполагается, что никакие элементы из таблицы не удаляются!)

Вот текст процедуры поиска hash-search(если элемент с ключом k со­держится в таблице Т в позиции j, процедура возвращает j, в противном случае она возвращает nil).

Листинг 4.5 – Процедура поиска элемента в таблице с открытой адресацией

Удалить элемент из таблицы с открытой адресацией не так просто. Если просто записать на его место NIL, то в дальнейшем мы не сможем найти те элементы, в момент добавления которых в таблицу это место было занято (и из-за этого был выбран более далёкий элемент в последовательности испробо­ванных мест). Возможное решение – записывать на место удалённого элемента не nil, а специальное значение deleted («удалён»), и при добавлении рассма­тривать ячейку с записью deleted как свободную, а при поиске – как занятую (и продолжать поиск). Недостаток этого подхода в том, что время поиска мо­жет оказаться большим даже при низком коэффициенте заполнения. Поэтому, если требуется удалять записи из хеш-таблицы, предпочтение обычно отдают хешированию с цепочками.

В нашем анализе открытой адресации мы будем исходить из предположения, что хеширование равномерно (uniform) в том смысле, что все m! перестановок множества {0,1,..., m – 1} равновероятны. На практике это вряд ли так, хо­тя бы по той причине, что для этого необходимо, чтобы число возможных ключей было как минимум ≤ m!, где m – число хеш-значений. Поэтому обычно пользуются более или менее удачными суррогатами, вроде описываемого ниже двойного хеширования.

Обычно применяют такие три способа вычисления последовательности испробованных мест: линейный, квадратичный и двойное хеширование. В каждом из этих способов последовательность á h (k, 0), h (k, 1),..., h (k, т – 1)ñ будет перестановкой множества {0,1,..., m – 1} при любом значении ключа k, но ни один из этих способов не является равномерным по той причине, что они дают не более m ² перестановок из m! возможных. Больше всего разных перестановок получается при двойном хешировании; не удивительно, что и на практике этот способ дает лучшие результаты.

const

В = {подходящая константа};

empty = ' '; {10 пробелов}

deleted = '**********'; {10 символов *}

c = 1; {шаг перебора}

MaxCase = {подходящая константа}; {Max количество попыток}

type

TypeElem = string[10]

HTableOpen = array[0..B-1] of TypeElem;

Теперь приведем сами алгоритмы на примере линейного опробования. Для остальных методов повторного хеширования алгоритмы идентичны.

procedure Clear_HTableOpen(var A: HTableOpen);

{Процедура очистки хеш-таблицы}

var

IndexSeg: integer;

begin

for IndexSeg:=0 to B-l do A[IndexSeg]:= empty;

end;

function Find_HTableOpen(x: TypeElem;

var A: HTableOpen;

var IndexSeg: integer): boolean;

{функция поиска элемента x в хеш-таблице. Принимает значение true, если найден и возвращает номер сегмента, в котором располагается найденный элемент, или принимает значение false и возвращает 0}

var

i: integer;

begin

i:= 0;

repeat

IndexSeg:= ((h(x) + c*i) mod B + {лин.опр.с цикл.переходом}

(h(x) + c*i) div B) {смещение после перехода}

mod B; {ограничение смещения}

i:= i + 1;

until (A[IndexSeg] = x) or {нашли}

(A[IndexSeg] = empty) or {дальше уже нет}

(i > MaxCase); {слишком долго ищем}

if A[IndexSeg] = x then begin

Find_HTableOpen:= true;

end else begin

Find_HTableOpen:= false;

IndexSeg:= 0;

end;

end;

function Add_HTableOpen(x: TypeElem;

var A: HTableOpen): boolean;

{Процедура добавления элемента x в хеш-таблицу. Возвращает true, если элемент добавлен, и false – в обратном}

var

i,

IndexSeg: integer; {номер сегмента}

begin

if not Find_HTableOpen(x, A, IndexSeg) then begin

{Если в таблице элемент уже есть, то добавлять не надо}

i:= 0;

repeat

IndexSeg:= ((h(x) + c*i) mod B +

(h(x) + c*i) div B)

mod B;

i:= i + 1;

until (A[IndexSeg] = empty) or {нашли место}

(A[IndexSeg] = deleted) or {тоже можно занять}

(i > MaxCase); {слишком долго ищем}

if (A[IndexSeg] = empty) or

(A[IndexSeg] = deleted) then begin

A[IndexSeg]:= x;

Add_HTableOpen:= true;

end else begin

Add_HTableOpen:= false;

end;

end

end;

procedure Del_HTableOpen(x: TypeElem; var A: HTableOpen);

{Процедура удаления элемента x из хеш-таблицы}

var

IndexSeg: integer; {номер сегмента}

begin

if Find_HTableOpen(x, A, IndexSeg) then begin

{Если в таблице элемент уже нет, то удалять не надо}

A[IndexSeg]:= deleted;

end

end;

Листинг 4.5 – Словарные операции при открытой адресации

Линейная последовательность проб

Пусть h': U ® {0,1,..., m – 1} – обычная хеш-функция. Функция, определяющая линейную последовательность проб (linear probing), задаётся формулой

h (k, i) = (h' (k) + i) mod т.

Иными словами, при работе с ключом k начинают с ячейки T [ h' (k)], а затем перебирают ячейки таблицы подряд: T [ h' (k)] + 1] ,T [ h' (k)+ 2],... (после Т [ т – 1 ] переходят к Т [0]). Поскольку последовательность проб полностью определяется первой ячейкой, реально используется всего лишь т различных последовательностей.

Открытую адресацию с линейной последовательностью проб легко реализовать, но у этого метода есть один недостаток: он может привести к образованию кластеров, то есть длинных последовательностей занятых ячеек, идущих подряд (по-английски это явление называется primary clustering). Это удлиняет поиск. На самом деле, если в таблице из m ячеек все ячейки с чётными номерами заняты, а ячейки с нечётными номерами свободны, то среднее число проб при поиске элемента, отсутствующего в таблице, есть 1,5. Если, однако, те же m / 2 занятых ячеек идут подряд, то среднее число проб примерно равно m / 8 = n / 4 (п – число занятых мест в таблице). Тенденция к образованию кластеров объясняется просто: если i заполненных ячеек идут подряд, вероятность того, что при очередной вставке в таблицу будет использована ячейка, следующая непосредственно за ними, есть (i + 1) / m, в то время как для свободной ячейки, предшественница которой также свободна, вероятность быть использованной равна всего лишь 1 / m. Всё вышеизложенное показывает, что линейная последовательность проб довольно далека от равномерного хеширования.

Квадратичная последовательность проб

Функция, определяющая квадратичную последовательность проб (quadraty probing), задаётся формулой

h (k, i) = (h’ (k) +c ₁ i + c ₂ i)mod m,

где, по-прежнему, h' – обычная хеш-функция, а с ₁и с ₂ – некоторые кон­станты. Пробы начинаются с ячейки номер T [ h' (k)], как и при линейном ме­тоде, но дальше ячейки просматриваются не подряд: номер пробуемой ячейки квадратично зависит от номера попытки. Этот метод работает значительно лучше, чем линейный, но если мы хотим, чтобы при просмотре хеш-таблицы использовались все ячейки, значения m, с ₁и с ₂нельзя выбирать как попало. Как и при линейном методе, вся последовательность проб определяется своим первым членом, так что опять получается всего т различных перестановок. Тенденции к образованию класте­ров больше нет, но аналогичный эффект проявляется в (более мягкой) форме образования вторичных кластеров (secondary clustering).

Двойное хеширование

Двойное хеширование (double hashing) – один из лучших методов открытой адресации. Перестановки индексов, возникающие при двойном хешировании, обладают многими свойствами, присущими равномерному хешированию. При двойном хешировании функция h имеет вид

h (k,i) = (h ₁(k) + i × h ₂(k)) mod т,

где h ₁и h ₂– обычные хеш-функции. Иными словами, последовательность проб при работе с ключом k представляет собой арифметическую прогрессию (по модулю m с первым членом h ₁(k) и шагом i × h ₂(k).

Чтобы последовательность испробованных мест покрыла всю таблицу, зна­чение h ₂(k)должно быть взаимно простым с m (если наибольший общий делитель h ₂(k)и m есть d, то арифметическая прогрессия по модулю т с разность h ₂(k)займёт долю 1 /d в таблице. Простой способ добиться выполнения этого условия – выбрать в качестве m степень двойки, а функцию h ₂взять такую, чтобы она принимала только нечётные значения. Другой вариант: m – простое число, значения h ₂–целые положительные числа, меньшие m. Например, для простого m можно положить

h ₁(k)= k mod m,

h ₂(k) = 1 + (k mod m'),

где т' чуть меньше, чем m (например, т' = т –1 или т –2). Если, например т = 701, т ¹ = 700 и k = 123456, то h ₁(k)= 80 и h ₂(k) = 257. Стало быть, последовательность проб начинается с позиции номер 80 и идёт далее с шагом 257 пока вся таблица не будет просмотрена (или не будет найдено нужное место).

В отличие от линейного и квадратичного методов, при двойном хешировании можно получить (при правильном выборе h ₁и h ₂)не m, a Q(m ²) различных перестановок, поскольку каждой паре (h ₁(k), h ₂(k))соответствует своя последовательность проб. Благодаря этому производительность двойного хеширования близка к той, что получилась бы при настоящем равномерном хешировании.

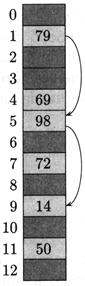
Рисунок 4.6 – Добавление элемента в таблицу с открытой адресацией при двойном хешировании

Рисунку 4.6 соответствует m = 13, h ₁(k) = k mod 13, h ₂(k) = 1+ (k mod 11). При выбранном k = 14 последовательность проб будет такая: 1-я и 5-я ячейки заняты, 9-я свободна, элемент «14» помещается туда.

Анализ хеширования с открытой адресацией

Так же, как и при анализе хеширования с цепочками, при анализе открытой адресации мы будем оценивать стоимость операций в терминах коэффициент заполнения a = п/т (п –число записей, т –размер таблицы). Поскольку при открытой адресации каждой ячейке соответствует не более одной записи, a £ 1.

Мы будем исходить из предположения о равномерности хеширования этой идеализированной схеме предполагается следующее: мы выбираем ключи случайным образом, причём все m!возможных последовательностей проб равновероятны. Поскольку эта идеализированная схема далека от реальности, доказываемые ниже результаты следует рассматривать не как математические теоремы, описывающие работу реальных алгоритмов открытой адресации, а как эвристические оценки.

Начнём с того, что оценим время на поиск элемента, отсутствующего в таблице.

Теорема 4.5. Математическое ожидание числа проб при поиске в с открытой адресацией отсутствующего в ней элемента не превосходит 1/(1 – a) (хеширование предполагается равномерным, через a < 1 обозначен коэффициент заполнения).

Доказательство. Мы предполагаем, что таблица фиксирована, а искомый элемент выбирается случайно, причём все возможные последовательности проб равновероятны. Нас интересует математическое ожидание числа попыток, необходимых для обнаружения свободной ячейки, то есть сумма

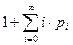
где p_i –вероятность того, что мы встретим ровно i занятых ячеек.

Каждая новая проба выбирается равномерно среди оставшихся не испробованными ячеек; если разрешить пробовать повторно уже испробованные ячейки, то часть проб пропадёт зря и математическое ожидание только увеличится. Но для этого нового варианта мы уже вычисляли математическое ожидание, и оно равно

1 / (1 – a)

поскольку вероятность успеха для каждой пробы равна 1 – a.

Если коэффициент заполнения отделён от единицы, теорема 4.5 предсказывает, что поиск отсутствующего элемента будет в среднем проходить за вре­мя О (1). Например, если таблица заполнена наполовину, то среднее число проб будет не больше 1/(1 – 0,5) = 2, а если на 90%, то не больше 1/(1 – 0,9) = 10.

Из теоремы 4.5 немедленно получается и оценка на стоимость операции добавления к таблице.

Следствие 4.6. В предположении равномерного хеширования математическое ожидание числа проб при добавлении нового элемента в таблицу с открытой адресацией не превосходит 1/(1 – a), где a < 1 – коэффициент заполнения.

Доказательство. При добавлении в таблицу отсутствующего в ней элемента происходят те же пробы, что при поиске отсутствующего в ней элемента.

Оценить среднее время успешного поиска немногим сложнее.

Теорема 4.7. Рассмотрим таблицу с открытой адресацией, коэффициент за­полнения которой равен a < 1. Пусть хеширование равномерно. Тогда матема­тическое ожидание числа проб при успешном поиске элемента в таблице не превосходит

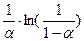
если считать, что ключ для успешного поиска в таблице выбирается случай­ным образом и все такие выборы равновероятны.

Доказательство. Уточним, как производится усреднение: сначала мы заполняем таблицу независимо выбираемыми ключами, причём для каждого из них выполняется предположение равномерного хеширования. Затем мы усредняем по всем элементам таблицы время их поиска.

Заметим, что при успешном поиске ключа k мы делаем те же самые пробы, которые производились при помещении ключа k в таблицу. Тем самым среднее число проб при поиске (усреднение по элементам) равно общему числу проб при добавлении, делённому на число элементов в таблице, которое мы обозначаем n. Математическое ожидание общего числа проб при добавлении равно сумме математических ожиданий для каждого отдельного шага. К моменту добавления (i +1)-го элемента в таблице заполнено i позиций, коэффициент заполнения равен i / т (т –число мест в таблице), и математическое ожидание не больше

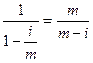
Поэтому сумма математических ожиданий не превосходит

+++…+

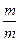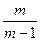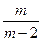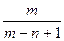
Эта сумма равна

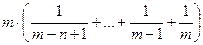
и оценивается сверxy с помощью интеграла:

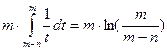
Вспоминая, что общее число операций надо поделить на n, получаем оценку

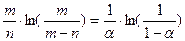
Если, например, таблица заполнена наполовину, то среднее число проб для успешного поиска не превосходит 1,387, а если на 90%, то 2,559.