2014-02-09
550
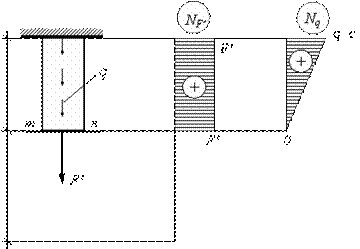
Рис.2.23
Для решения задачи используем принцип независимости действия сил, а именно: отдельно построим эпюры продольных сил от действия сосредоточенной силы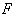 
и от действия собственного веса, то есть от равномерно распределенной продольной нагрузки 
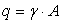. Расчетная схема и эпюры продольных сил 
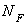и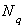 
изображены на рис. 2.23.
Полное удлинение стержня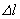 
будет складываться из удлинения, полученного стержнем от действия сосредоточенной силы 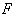и от действия собственного веса:
.
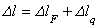Или в другом виде:
.
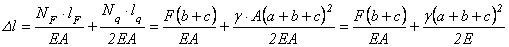Для того, чтобы определить перемещение сечения m-n отбрасываем часть стержня ниже сечения m-n, а ее действие заменяем сосредоточенной силой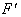 
, равной продольной силе в сечении m-n:
.
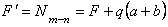В результате получаем новую расчетную схему, которая приведена на рис. 2.24.
