2014-02-09
750
Рис.2.22
Рис.2.21
Максимальная сжимающая продольная сила возникает у основания опоры и определяется выражением (для удобства будем подставлять значения внутренних усилий по абсолютной величине):
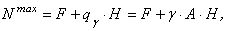
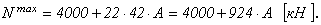
Записываем условие прочности:
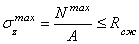
Подставляя в это выражение значение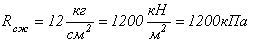 
получим:
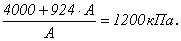
Отсюда требуемая площадь из условия прочности кладки на сжатие равна:
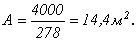
Объем кладки для первого варианта будет равен:
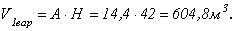
2 вариант. Расчетная схема и эпюра внутренних усилий для данного варианта изображена на рис. 2.22.
Мостовая опора состоит из трех ступеней, высота каждой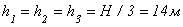 
. Площади поперечных сечений ступеней соответственно 
, 
, 
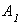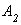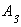, в связи с чем в пределах каждой ступени от действия собственного веса будут возникать различные по величине продольные силы и напряжения.
Таким образом, для решения задачи необходимо рассмотреть условие прочности для каждой ступени отдельно.
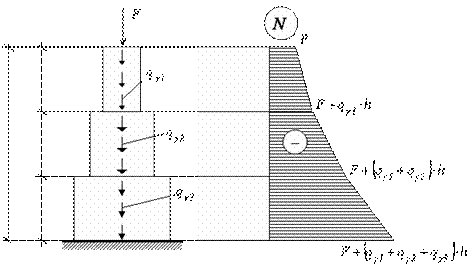
1-я ступень. Максимальная сжимающая продольная сила для первой ступени (рис. 2.22):
.
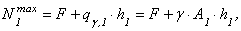
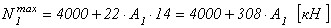По аналогии с вариантом 1, записываем для первой ступени условие прочности и подставляем в него исходные данные:
.
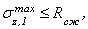
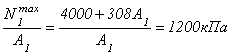Отсюда требуемая площадь первой ступени равна:
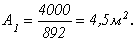
2-я ступень. Максимальная сжимающая продольная сила для второй ступени (рис. 2.22):
.
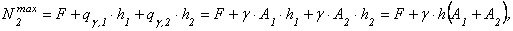
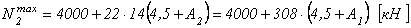Записываем для второй ступени условие прочности и подставляем в него исходные данные:
.
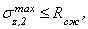
Отсюда требуемая площадь второй ступени равна:
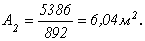
3-я ступень. Максимальная сжимающая продольная сила для третьей ступени (рис. 2.22):
.
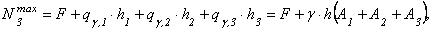
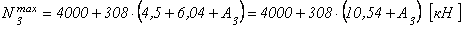Записываем для третьей ступени условие прочности, из которого по аналогии с предыдущими записями определяем требуемую площадь поперечного сечения:
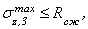
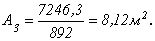
Объем кладки мостовой опоры для второго варианта определяется выражением:
.
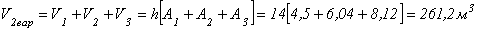Таким образом, мостовая опора, состоящая из ступеней различной площади, выгоднее по расходу материала, чем опора постоянного по всей высоте сечения.
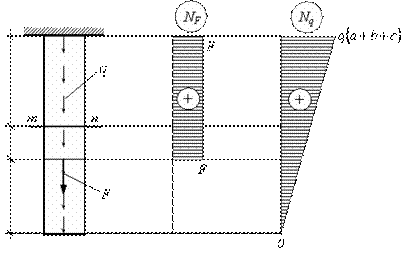
Определить полное удлинение стержня, с учетом собственного веса, а также перемещение сечения m-n. Площадь поперечного сечения – А, модуль упругости – Е, объемный вес материала -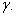 
Расчетная схема стержня изображена на рис. 2.23.
