 f(x1,x2)
f(x1,x2)

x2
x1
Условия определяющие точку минимума – необходимо проанализировать поведение функции в некоторой точке.
 |
х2
 |
 х2
х2
Часто под окрестностью подразумевают шар.
Рассмотрим вспомогательное построение:
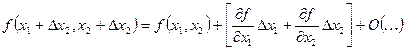
линейное векторное  x3
x3
 пространство
пространство
 |

 (х1,х2,х3)
(х1,х2,х3)
 |
x2
x1
Скалярное произведение векторов 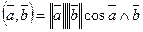 , где
, где 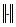 - длина вектора (норма вектора),
- длина вектора (норма вектора), 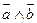 - угол между векторами.
- угол между векторами.

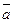 S
S
 |
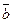
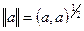
Допустим, что: 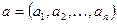 ,
, 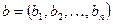
Тогда: 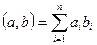 ;
; 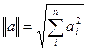
Допустим, что имеется 2 вектора:




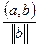
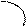 a
a

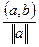
Чтобы задать направление, мы задаем вектор.


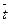 Нормируем вектор
Нормируем вектор 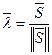
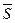
Нормированный вектор имеет тоже самое направление, но 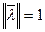 , длина.
, длина.
Допустим, что задан нормированный вектор 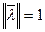 .
.
отрицательный |
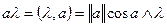 Скалярное произведение равно 0, тогда года
Скалярное произведение равно 0, тогда года 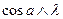 прямой. прямой.
|
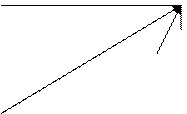
Возвращаемся к функции 2-х переменных:
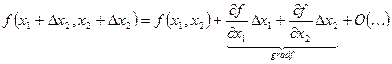
Отбрасываем члены 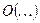 , приращение будет более точным.
, приращение будет более точным.
 х2 х2
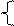    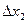
   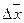
х1
|
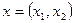
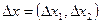
|
Вектор  Þ
Þ 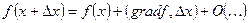 - формула Тейлора.
- формула Тейлора.
х1 |
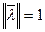 Мы рассматриваем как изменяется точка вдоль данного направления.
Функция становится функцией одной переменной.
Мы рассматриваем как изменяется точка вдоль данного направления.
Функция становится функцией одной переменной.
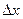 - скалярная величина. - скалярная величина.
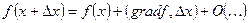
|
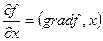 - производная по направлению (вдоль данного направления)
- производная по направлению (вдоль данного направления)
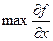 - направление ряда равное направлению grad (£ 0).
- направление ряда равное направлению grad (£ 0).
grad – вектор, в сторону которого функция изменяется более быстро.
Антиградиент – grad направленный в другую сторону (-grad).
 х2 х2
 grad f grad f
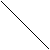 f(x) f(x)
 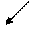   х2
-grad f х2
-grad f
х1 х1 |
Необходимое условие:
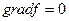 - локальный минимум (или максимум). Точки локального экстремума. - локальный минимум (или максимум). Точки локального экстремума.
|
Допустим что мы совершаем малое перемещение 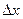 . В каком случае (в точке) будет: * больше, чем заданная: тогда, когда угол – острый Þ
. В каком случае (в точке) будет: * больше, чем заданная: тогда, когда угол – острый Þ 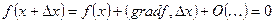 .
.
* - если под прямым углом, то не изменяется;
* - если под тупым углом, то приводит к уменьшению функции.
1. 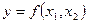
строим поверхности
 z
z

 y
y
 2014-02-09
2014-02-09 405
405






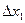


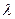

 х2
х2 







