Численное решение:
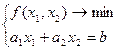
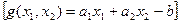
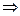 точка min должна лежать на прямой.
точка min должна лежать на прямой.
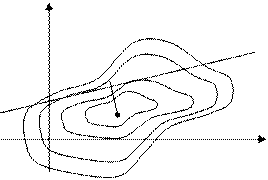
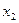
g(x)
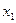
В каждый момент линия уровня будет касаться прямой 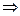 эта точка и является точкой
эта точка и является точкой
условного локального min. Если в окрестности заданной точки, удовлетворяющей
всем значениям равенства, значение функции больше, чем в точке, то эта точка – есть точка условного локального min.
Пример:
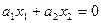
(a,x)=0
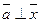
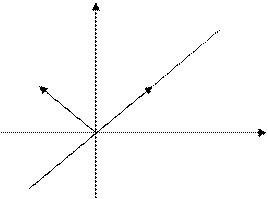
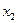
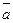
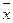
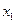
Если (a1x)=b
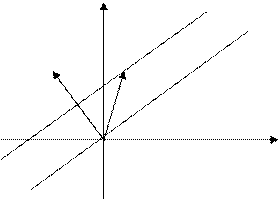
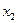
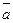
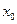
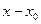
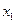
Допустим, 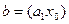

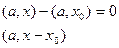
Прямая будет проходить через некоторую точку удовлетворяющую условию и 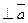
Для n переменных 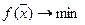 , Ax=b
, Ax=b
Рассмотрим i-ое ограничение:
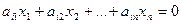 ,
, 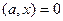
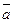 - задан
- задан 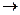 x - все вектора, лежащие
x - все вектора, лежащие  . Они и составляют гиперплоскость.
. Они и составляют гиперплоскость.
При добавлении еще одного условия, уменьшаются размерности. В конечном итоге получится пространство n-m.
Для двух переменных возможно 2 случая:
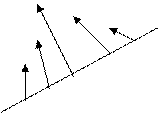 1. 1.
| 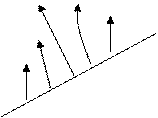 2. 2.
|
В случае 2 это не точка минимума, а седловая точка.
Рассмотрим точку 3-х переменных:
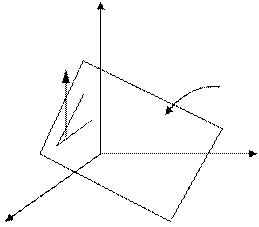  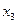
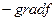 плоскость
плоскость
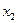
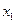
| Ограничение – плоскость, следовательно, все допустимые точки на плоскости. Если угол grad не равен 90 градусам следовательно можно двигаться дальше. На плоскости существует направление, которое будет составлять острый угол с – grad, и двигаясь в этом направлении можно уменьшить значение f. Если -grad f перпендикулярен плоскости эта точка может быть точкой минимума. |
Пусть существует 2 ограничения:
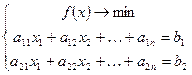
Рассмотрим опять случай 3-х переменных:
Точка минимума должна принадлежать пересечению плоскостей.
Необходимое условие – вектор антиградиента должен составлять угол 90 градусов с прямой пересечения плоскостей.
Для п -мерного случая имеется п переменных следовательно рассматривая каждое ограничение, получаем п-1 гиперплоскость следовательно рассмотрев т ограничений получим п-т гиперплоскость (т<п).
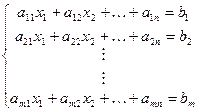
|
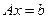 все ограничения
независимы
все ограничения
независимы
|
Если вектор grad (п -мерный) будет ортогонален п-т – пространству.
Допустим имеется п-1 пространство, п -мерный вектор может принадлежать ему или нет. Пусть вектор не принадлежит данному подпространству следовательно его можно разложить на 2 вектора – один который принадлежит подпространству, и второй который ортогонален данному. Ортогональное дополнение – вектора, которые ортогональны данному подпространству.
В 3D – пространстве, если подпространство равно 1 следовательно ортогональное дополнение равно 2.
В п-т -мерном подпространстве ортогональное дополнение имеет размерность т.
Необходимое условие: Если мы находим точку, где вектор градиента принадлежит ортогональному дополнению к пространству, заданному ограничениями – равенствами, то эта точка может быть точкой локального минимума.
Пусть есть 2 плоскости. Если записать систему ограничений равенств следующим образом:
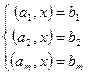
где 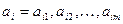
Т.о. вектора 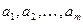 порождают ортогональное дополнение. Существующие могут быть выбраны в качестве базиса ортогонального дополнения следовательно градиент принадлежит ортогональному дополнению:
порождают ортогональное дополнение. Существующие могут быть выбраны в качестве базиса ортогонального дополнения следовательно градиент принадлежит ортогональному дополнению:
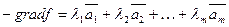
т.е. линейная комбинация базисных векторов.
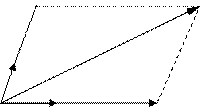 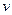
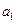
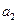
|
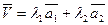
|
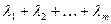 - множители Лагранжа.
- множители Лагранжа.
Рассмотрим матрицу 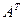 , в ней
, в ней 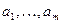 - столбцы.
- столбцы.
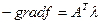
это условие может быть использовано для численного решения задачи оптимизации с ограничивающими уравнениями.
Пример: 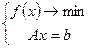
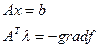
Если найдем такие вектора х и 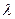 , для которых эти условия выполняются то точка может быть точкой локального минимума.
, для которых эти условия выполняются то точка может быть точкой локального минимума.
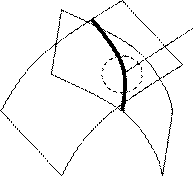
Рассмотрим случай когда система ограничений – равенств нелинейная:
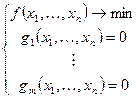
|
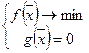
|
Если функции дифференцируемы, то в окрестности точки минимума они будут вести себя как линейные.
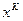
|
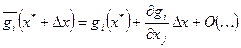 следовательно в окрестности точки локального минимума эта зависимость линейная следовательно получается система вида: следовательно в окрестности точки локального минимума эта зависимость линейная следовательно получается система вида:
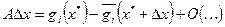 , где , где 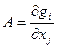
|
следовательно необходимое условие локального минимума:
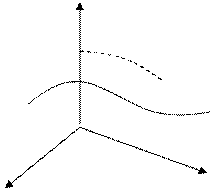
n-m
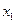
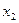
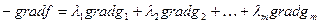
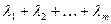 - множители Лагранжа.
- множители Лагранжа.
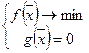
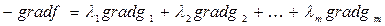
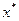 - точка может быть искомой в задаче
- точка может быть искомой в задаче
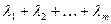 - множители Лагранжа.
- множители Лагранжа.
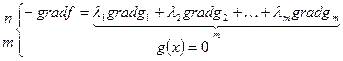
Обозначения для скалярного произведения 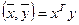 ;
;
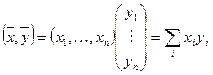 ;
;
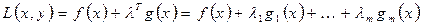
Необходимое условие точки локального минимума исходное задание с ограничениями представляет собой необходимое условие точки локального экстремума для функции Лагранжа.
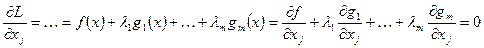
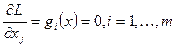
 2014-02-09
2014-02-09 612
612








