 - заданные функции нелинейные
- заданные функции нелинейные
НЛП 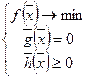
Рассмотрим 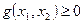
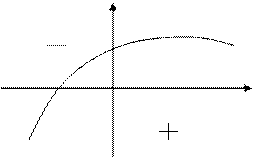
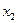
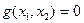
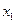
Пример:
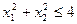
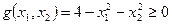

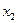
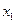
В случае системы неравенств пересечение всех областей. Если g > 0, то ограничение неравенства – неактивно (точку можно смещать).
Если точка точно на границе, то говорят, что ограничение активно.
Рассмотрим случай:
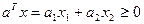
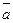
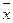
|
Если задано линейное ограничивающее неравенство, то вектор 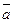 направлен внутрь допустимой области. Если направлен внутрь допустимой области. Если 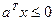 , то вектор , то вектор 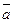 будет направлен из допустимой области. будет направлен из допустимой области.
|
Если 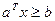 , то граница проходит не через начало координат.
, то граница проходит не через начало координат.
Необходимые условия:
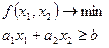
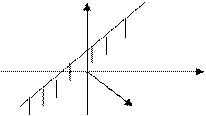 |
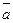
- Если локальный минимум внутри допустимой области, то
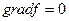 ;
; - Если точка локального минимума точно на границе, то
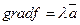 , точка является точкой локального, если
, точка является точкой локального, если 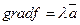 и
и 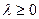
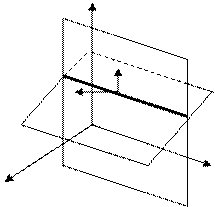
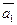
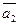
|
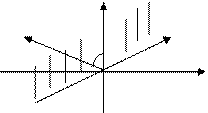
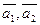 - вектора нормали к соответствующей плоскости. - вектора нормали к соответствующей плоскости.
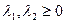
|
В общем случае:
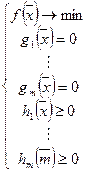
а) 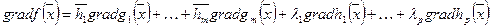 ;
;
б) 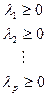 ;
;
в) Если 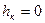 , то
, то 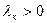 . Если
. Если 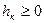 , то
, то 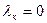 . Т.е.
. Т.е. 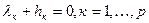 . Условие дополняющей нежесткости.
. Условие дополняющей нежесткости.
Все 3 условия в совокупности называются условиями Куна-Таккера (условия оптимальности первого порядка).
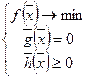
| Ограничения неравенства
|
 Можно записать и так:
Можно записать и так:
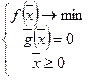
Поскольку постановка задачи 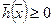
 |  | ||
Основные результаты:
Область п -мерного пространства называется выпуклой если вместе с 2-ми точками, она содержит весь отрезок, соединяющий эти 2 точки.
Пример:
Функция нескольких переменных 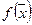 называется выпуклой если ее матрица Гесса положительно определена.
называется выпуклой если ее матрица Гесса положительно определена.
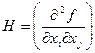 ;
; 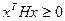
 Если мы рассматриваем неравенство
Если мы рассматриваем неравенство 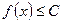 , то данное неравенство определяет выпуклую область.
, то данное неравенство определяет выпуклую область.
область будет выпуклой
Th: Пусть дана задача НЛП, если целевая функция этой задачи – выпуклая, и область целевых решений так же выпукла, то локальный оптимум совпадает с ее глобальным оптимумом задачи (задачи выпуклого программирования).
1 случай – когда все ограничительные неравенства являются не активными.
2 случай – когда точка лежит на границе.
Методы решения НЛП.
| |||||
| Нулевого порядка – поисковые методы (безусловные ориентиры похожи на это). Используется только значение целевой функции (Z). | Первого порядка – аналогичны градиентным методам. Условно градиентные методы. Используется и Z и вектор градиента (grad Z). | Второго порядка. Ньютоновские методы. Они являются специальными вариантами методов Ньютона для оптимизации. Используется Z, grad Z и матрица Гесса (Н) | |||
(*)
|  (**) (**)
| (***)
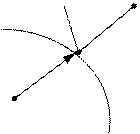 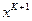
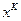
|
(**)
1 случай – вектор grad направлен по нормали;
2 случай – идет под углом (надо спроецировать поверхность следовательно она будет показывать направление)
Если мы внутри, двигаемся как в (*), а далее (**). Это более эффективный метод.
(***)
Рассмотреть отрезок, это может дать нам еще один отрезок.
 2014-02-09
2014-02-09 561
561