Моделирование поведения облака газообразной примеси в пограничном слое атмосферы
Постановление или определение суда кассационной инстанции вступает в законную силу со дня его принятия

Загрязняющие атмосферу вещества распространяются в воздушном потоке за счет турбулентных движений воздушных масс, имеющих стохастический характер. За счет этого в каждой точке облака в фиксированные моменты времени значения мгновенной концентрации примеси представляют собой случайные величины, основной характеристикой которых является функция распределения. По полному множеству статистических моментов можно восстановить функцию распределения. Ограниченный набор статистических моментов позволяет найти приближенную форму функции распределения.
Многочисленные наблюдения показали, что с достаточной для практических целей точностью функция распределения значений мгновенной концентрации газоаэрозольной примеси может быть представлена нормальным распределением или гауссовской функцией. В этом случае необходимо определить первые два статистических момента – математическое ожидание  мгновенной концентрации примеси
мгновенной концентрации примеси 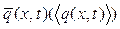 или «осредненную мгновенную концентрацию» и среднее квадратичное отклонение мгновенной концентрации примеси от ее математического ожидания
или «осредненную мгновенную концентрацию» и среднее квадратичное отклонение мгновенной концентрации примеси от ее математического ожидания 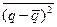 или «дисперсию распределения случайной величины мгновенной концентрации».
или «дисперсию распределения случайной величины мгновенной концентрации».
Если точность описания распределения мгновенной концентрации примеси нормальным законом недостаточна. То эту функцию распределения можно уточнить с помощью статистических моментов третьего, четвертого и т.д. порядка с помощью ряда Ле-Шателье.
С помощью полуэмпирической теории турбулентности для пограничного слоя атмосферы можно построить математические модели для определения статистических моментов. Так для математического ожидания мгновенной концентрации примеси можно записать уравнение параболического типа в виде
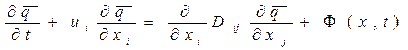 (1)
(1)
Здесь
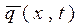 - значение математического ожидания случайной величины мгновенной концентрации примеси в точке
- значение математического ожидания случайной величины мгновенной концентрации примеси в точке 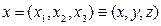 в момент времени t;
в момент времени t;
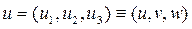 - вектор скорости ветра (скорости воздушного потока) в точке x в момент времени t;
- вектор скорости ветра (скорости воздушного потока) в точке x в момент времени t;
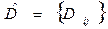
 - коэффициент турбулентной диффузии, представляет собой тензор второго ранга;
- коэффициент турбулентной диффузии, представляет собой тензор второго ранга;
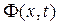 - функция, описывающая распределение в пространстве и во времени мощности выброса примеси в атмосферу.
- функция, описывающая распределение в пространстве и во времени мощности выброса примеси в атмосферу.
Для дисперсии мгновенной концентрации примеси в рамках полуэмпирической теории
турбулентности можно получить следующее дифференциальное уравнение:

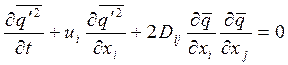 . (2)
. (2)
Решение этих двух дифференциальных уравнений полностью описывают в рамках нормального закона распределения статистические характеристики газоаэрозольного облака в воздушном потоке пограничного слоя атмосферы.
Начально-краевая задача. Для того чтобы получить однозначное решение уравнения (1) и (2) необходимо поставить начальное условие (задача Коши) и краевые условия (задача Штурма - Лиувилля).
Задача Коши для уравнения (1) в наиболее общем виде может быть представлена как
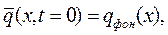
где 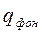 - фоновые значения концентрации рассматриваемой примеси.
- фоновые значения концентрации рассматриваемой примеси.
Без потери общности можно положить значения фоновой концентрации равные нулю и записать задачу Коши для уравнения (1) следующим образом
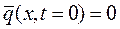 (3)
(3)
Задача Штурма-Лиувилля для уравнения (1) может быть записана в следующем виде:
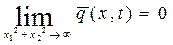 (4)
(4)
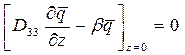 (5)
(5)
где β- скорость осаждения примеси на подстилающую поверхность;
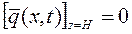 (6)
(6)
где Н – высота «слоя диффузии».
Дополнительные условия для моделирования. При моделировании поведения газоаэрозольного облака ограничимся ситуацией, когда облако переносится над однородной поверхностью земли на относительно небольшие расстояния порядка 100 км. Для таких ситуаций время переноса примеси составляет несколько часов (5 час), в течении этого времени состояние пограничного слоя атмосферы изменяется незначительно. Таким образом, дополнительным условием для моделирования распространения облака примеси является ограничение на характер атмосферного течения в пограничном слое атмосфере, а именно будем рассматривать горизонтально однородное стационарное атмосферное течение, т.е. все его параметры такие, как вектор скорости, температура воздуха, напряжения Рейнольдса (параметры турбулентного обмена) и т.д. изменяются только с высотой, т.е. зависят только от вертикальной координаты z.
Для таких условий распространения примеси уравнение турбулентной диффузии запишется в следующем виде:
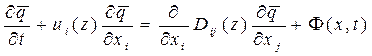 (7)
(7)
где 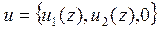 ,
,
с начально-краевой задачей
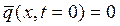 (8)
(8)
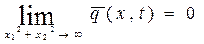
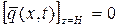
Для конкретизации алгоритмов математического моделирования поведения газообразных облаков без потери общности в качестве функции мощности источника можно выбрать функцию для точечного мгновенного источника, т.е.
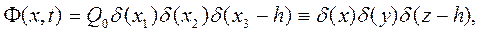 (10)
(10)
где (0,0,h) – координаты точечного источника;
 - количество выброшенной в атмосферу примеси;
- количество выброшенной в атмосферу примеси;
Если известно решение задачи для точечного мгновенного источника, то решение задачи для источника, мощность которого описывается функцией Ф(x,t), можно найти с помощью интеграла-свертки:
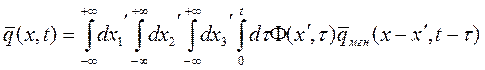 (11)
(11)
где 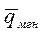 - решение задачи для мгновенного источника примеси.
- решение задачи для мгновенного источника примеси.
 2014-02-09
2014-02-09 453
453







