Для уравнения (1.3) начально-краевая задача имеет вид:
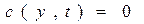 (14)
(14)
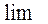
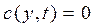
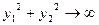
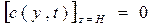

Уравнение (13) относится к классу параболических уравнений, решение которых принадлежит линейному функциональному пространству функций, интегрируемых с квадратом, т.е.
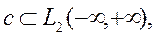
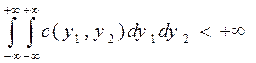
В функциональном пространстве  имеется фундаментальный базис, образованный функциями
имеется фундаментальный базис, образованный функциями

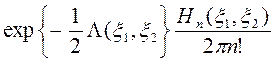 ,
,
где
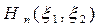 - двухмерные полиномы Эрмита, в которых
- двухмерные полиномы Эрмита, в которых 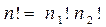 ;
;
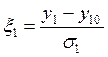 ;
; 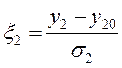 ;
;
Квадратичная форма 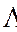 может быть представлена в виде
может быть представлена в виде
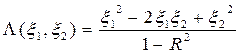
Любую функцию из 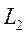 , в том числе и решение уравнения диффузии (13), можно разложить по фундаментальному базису, т.е. записать как
, в том числе и решение уравнения диффузии (13), можно разложить по фундаментальному базису, т.е. записать как
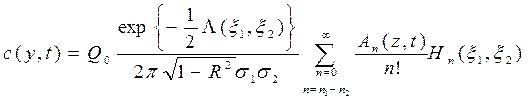 (15)
(15)
Здесь 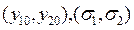 - параметры, которые характеризуют распределение массы примеси в горизонтальных сечениях облака в фиксированные моменты времени. Так параметры
- параметры, которые характеризуют распределение массы примеси в горизонтальных сечениях облака в фиксированные моменты времени. Так параметры 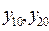 представляют собой координаты положения центра тяжести распределенной в горизонтальном сечении облака массы примеси.
представляют собой координаты положения центра тяжести распределенной в горизонтальном сечении облака массы примеси.
Для выяснения физического смысла параметров 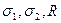 предположим, что в горизонтальных сечениях облака масса примеси распределена в соответствии гауссовского закона. В этом случае
предположим, что в горизонтальных сечениях облака масса примеси распределена в соответствии гауссовского закона. В этом случае 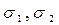 - дисперсии такого гауссовского распределения, а параметр R – определяет направление главных осей эллипсов равных концентраций (изоконцентраций) в плоскости
- дисперсии такого гауссовского распределения, а параметр R – определяет направление главных осей эллипсов равных концентраций (изоконцентраций) в плоскости 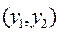 . С механической точки зрения параметры
. С механической точки зрения параметры 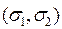 представляют собой моменты инерции распределенной массы.
представляют собой моменты инерции распределенной массы.
Двухмерные полиномы Эрмита. Двухмерные полиномы Эрмита определяются через свою  производящую функцию как
производящую функцию как
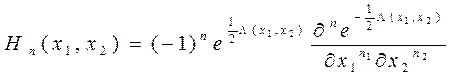 (17)
(17)
где  -
-  мультииндекс, т.е.
мультииндекс, т.е. 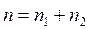 .
.
Функции (полиному) Эрмита можно поставить в соответствие сопряженные полиномы Эрмита 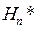 , определив их через производящую функцию как
, определив их через производящую функцию как
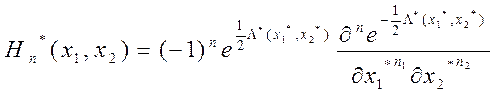 (18)
(18)
Здесь сопряженные переменные 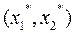 и сопряженная квадратичная форма
и сопряженная квадратичная форма 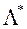 имеют следующий вид:
имеют следующий вид:
 ;
; 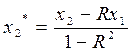 ;
;
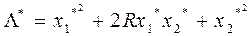 .
.
Полиномы Эрмита обладают свойством ортогональности, которое можно представить в виде следующего соотношения:
(19)
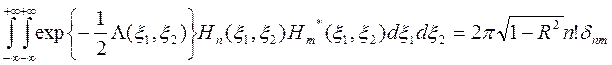
где 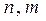 - мультииндексы;
- мультииндексы; 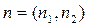 ;
; 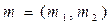 ;
;
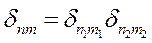 - мультисимвол Кронекера.
- мультисимвол Кронекера.
В Таблице №1 приведены выражения для двухмерных полиномов Эрмита, в Таблице № 2 – аналогичные сопряженные полиномы.
Коэффициенты разложения. Коэффициенты разложения интегрируемой с квадратом функции по ортогональному базису линейного функционального пространства 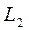 можно определить с помощью 2соотношения ортогональности двухмерных полиномов Эрмита. Коэффициенты
можно определить с помощью 2соотношения ортогональности двухмерных полиномов Эрмита. Коэффициенты 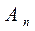 в этом случае примут следующий вид:
в этом случае примут следующий вид:
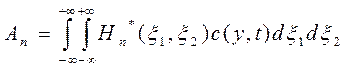 (20)
(20)
Степенные моменты. Степенные моменты 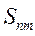 , которые определяются как
, которые определяются как
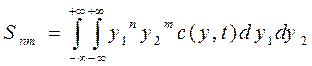 ,
, 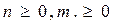 ,
,
появляются в рассматриваемой задаче тогда, когда в выражении (20) для коэффициентов разложения функции по ортогональному базису линейного функционального пространства 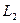 полиномы Эрмита заменяются их явными выражениями.
полиномы Эрмита заменяются их явными выражениями.
Наряду со степенными моментами 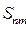 , которые принято называть начальными степенными моментами, применяются центральные степенные моменты
, которые принято называть начальными степенными моментами, применяются центральные степенные моменты 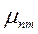 , определяемые следующим образом:
, определяемые следующим образом:
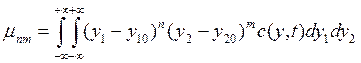 (21)
(21)
Через степенные моменты можно определить основные параметры распределения массы примеси. Так, координаты положения центра тяжести распределенной в горизонтальных сечениях облака массы примеси можно определить как:
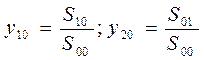 (22)
(22)
Для дисперсии распределенной массы примеси связь со степенными моментами имеет следующий вид:
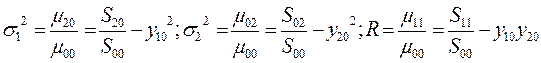 (23)
(23)
Связь с коэффициентами разложения 
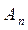 приведены в следующей таблице:
приведены в следующей таблице:
 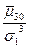
| 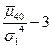
| ||||
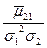
| 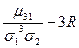
| ||||
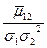
| 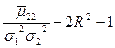
| ||||
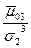
| 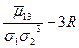
| ||||
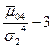
|
Здесь 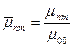 .
.
Таким образом, определив набор степенных моментов (начальных или центральных) мы находим распределение математического ожидания мгновенной концентрации примеси в пространстве и во времени.
 1.3. Степенные моменты
1.3. Степенные моменты
Начально-краевая задача для степенных моментов. Из исходного уравнения диффузии (13) и соотношения (21) можно получить соответствующие уравнеия для степенных моментов. Аналогичным образом из начально-краевых условий (14) для искомой функции 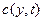 можно получить начально-краевые условия для степенных моментов.
можно получить начально-краевые условия для степенных моментов.
Для момента нулевого порядка начально-краевая задача имеет вид:
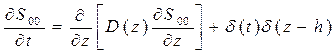
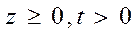 (25)
(25)
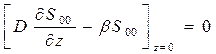
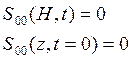
Уравнения для начальных степенных моментов первого порядка имеют следующий вид
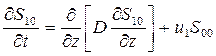 (26)
(26)
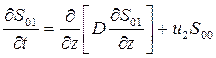
Центральные моменты первого порядка тождественно равны нулю.
Уравнения для начальных степенных моментов второго порядка имеют следующий вид
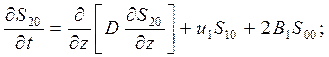
(27)
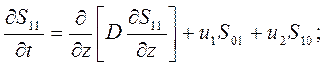
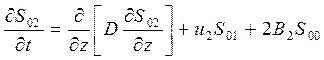 .
.
Аналогичное уравнение для центральных моментов можно представить в следующем виде:
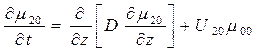 ; (28)
; (28)
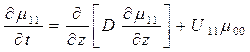 ;
;
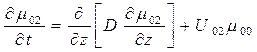
Здесь 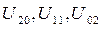 имеют следующий вид
имеют следующий вид
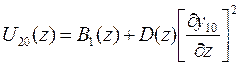 ;
;
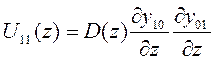 ;
;
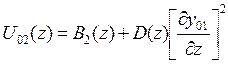 .
.
Для начальных степенных моментов третьего порядка соответствующие уравнения имеют
вид:
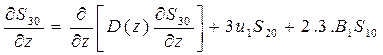 ;
;
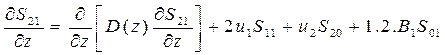 ;
;

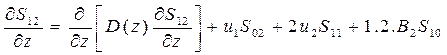 ;
;
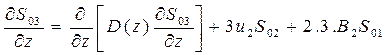 .
.
Соответствующие уравнения для центральных моментов третьего порядка можно записать следующим образом:
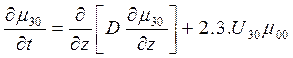 ; (30)
; (30)
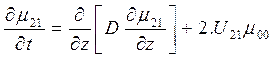 ;
;
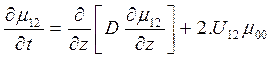 ;
;
. 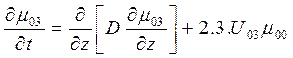
Здесь функции 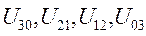 имеют вид:
имеют вид:
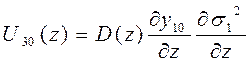 ;
;
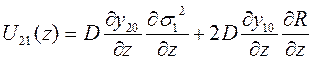 ;
;
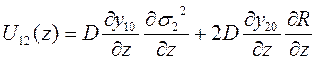 ;
;
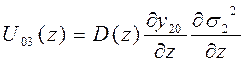 .
.
Уравнения для начальных и центральных степенных моментов можно записать как
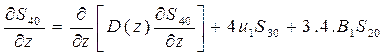
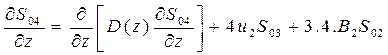
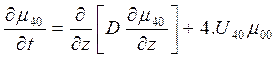 (31)
(31)
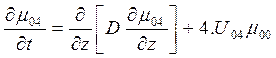
Здесь
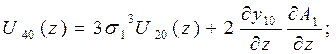
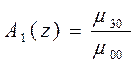
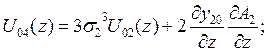
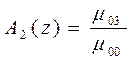
Начальные и краевые условия для степенных моментов можно записать следующим:
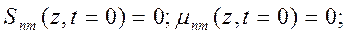 (32)
(32)
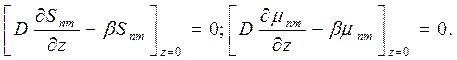
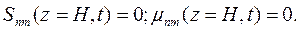
Таким образом, для определения центральных степенных моментов 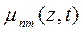 необходимо найти решение дифференциального уравнения
необходимо найти решение дифференциального уравнения
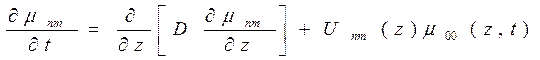
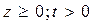 , удовлетворяющее нулевому начальному условию, т. е.
, удовлетворяющее нулевому начальному условию, т. е.
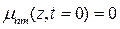 ,
,
и краевым условиям
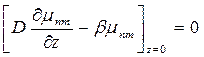 .
.
Решение этого уравнения, удовлетворяющее начально-краевой задачи, можно выразить с помощью функции Грина следующим образом:
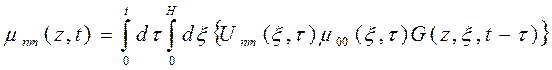 (37)
(37)
Функция Грина 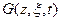 по определению является решением следующей задачи:
по определению является решением следующей задачи:
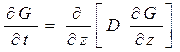 ,
, 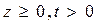 (38)
(38)
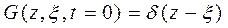
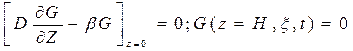
Очевидно, что 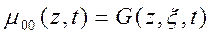 .
.
Это позволяет представить выражение (37) следующим образом:
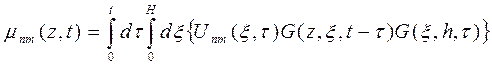
Таким образом, задача об определении центральных степенных моментов сводится к решению задачи для функции Грина.
1.4. Функция источника (функция Грина)
1.4.1. Функция источника для диффузионной задачи определим как решение уравнения
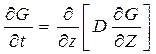 ,
,
определенное на полупрямой 0<z< , ограниченное при t>0, удовлетворяющее начальному условию
, ограниченное при t>0, удовлетворяющее начальному условию
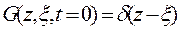

и одному из краевых условий
- краевое условие 1-ого рода
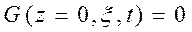 ;
;
- краевое условие 2-ого рода
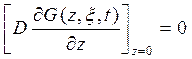 .
.
1.4.2. Выберем вспомогательную функцию U, определенную на прямой 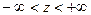 , удовлетворяющую уравнению
, удовлетворяющую уравнению
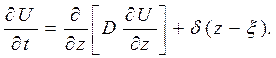
Для того, чтобы эта функция была продолжением функции G на отрицательную полуось
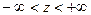 , она должна удовлетворять начальному условию
, она должна удовлетворять начальному условию
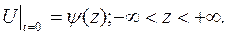
Если рассматривается краевое условие 1-ого рода, функция 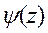 должна быть нечетной, т. е.
должна быть нечетной, т. е.
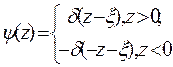
Если рассматривается краевое условие 2-ого рода, функция 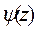 должна быть четной, т.е.
должна быть четной, т.е.
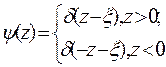
В этом случае функцию источника, определенную на полупрямой 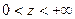 и удовлетворяющую краевому условию!-ого рода можно представить как
и удовлетворяющую краевому условию!-ого рода можно представить как
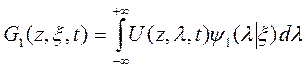
Для функции, удовлетворяющей краевому условию 2-ого рода, имеем
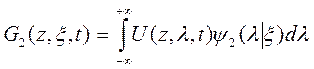

1.4.3. К уравнению для вспомогательной функции U применим преобразование  Лапласа
Лапласа
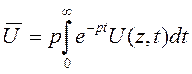
и получим

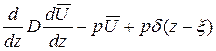
Решение этого уравнения будем искать в виде
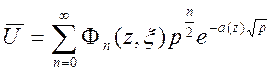 ,
, 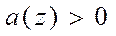
Подставив это выражение в уравнение для вспомогательной функции и приведя подобные члены, получаем
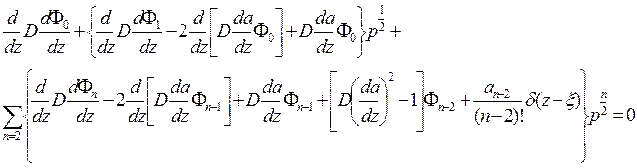
Приравнивая к нулю члены при одинаковых степенях р:
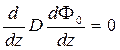
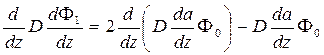
……………………………………………………..
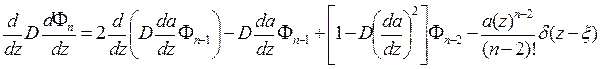
Функцию 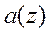 определим так, чтобы
определим так, чтобы
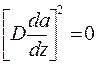
В этом случае для 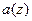 получим следующее выражение
получим следующее выражение
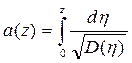 ;
; 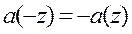
Первые два уравнения имеют нулевые решения, т.е. 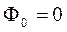 и
и 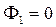 . Для функции
. Для функции 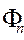 можно записать следующее выражение:
можно записать следующее выражение:
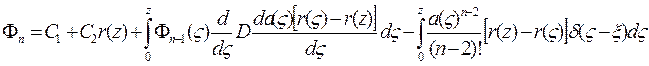
где
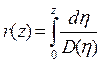 - сопротивление слоя диффузии
- сопротивление слоя диффузии 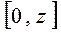 .
.
Из условия 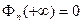 получаем
получаем
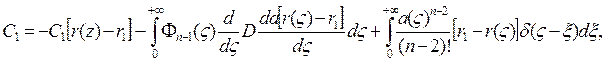
где 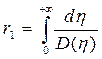 .
.
Из условия  =0 получаем
=0 получаем
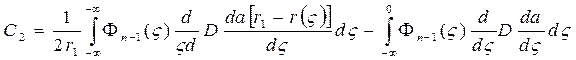
+
в
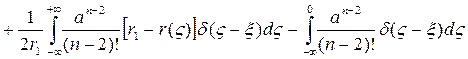
Теперь функцию 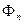 можно представить в виде:
можно представить в виде:
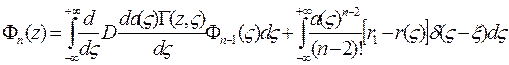
где
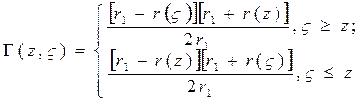

Функция 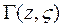 является решением уравнения:
является решением уравнения:
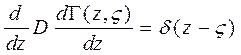
Лемма: 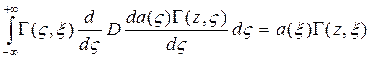
С учетом этого соотношения функции 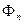 можно представить в виде:
можно представить в виде:
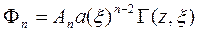
Для определения коэффициентов 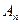 имеем соотношение
имеем соотношение
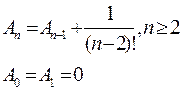
Отсюда имеем
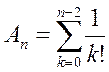
Теперь функция 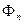 примет вид
примет вид
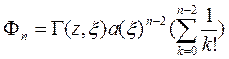
Образ Лапласа вспомогательной функции 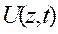 примет вид
примет вид
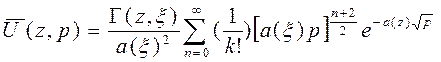

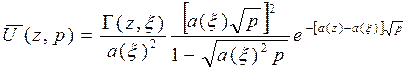
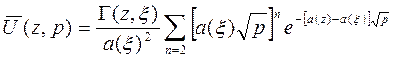
Используя следующее соотношение:
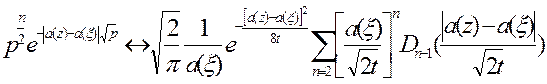
Вспомогательную функцию теперь можно записать следующим образом
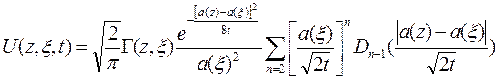
1.4.4. Для функции источника, удовлетворяющей первому краевому условию, запишем следующее выражение
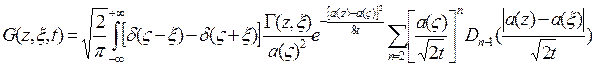
или
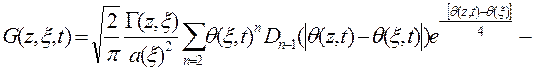
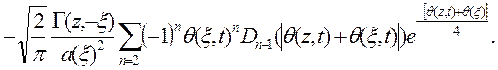
1.4.5. Для функции источника, удовлетворяющей второму краевому условию, можно записать следующее выражение
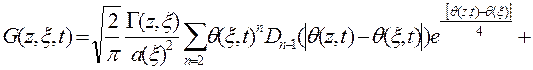
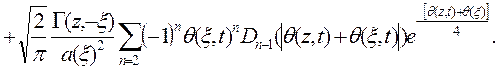
Здесь 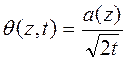
 2014-02-09
2014-02-09 640
640







