2014-02-09
882
06.02.2012.
Приложение 3. Схема анализа календарного плана воспитательно-образовательной работы в группе детского сада
Список литературы
Примеры программ
Половинное деление
int Find(int *array, int size)
{
int a = 0,b = size-1,t;
do
{
t = (b+a)/2;
if (m[t] == x)return t;
if (m[t]>x) b = t;
else a = t;
}while (b-a>1);
if (m[a] == x) return a;
if (m[b] == x) return b;
return -1;
}
Сортировка пузырьком
int t;
char flag;
do
{
flag = 0;
for(int i=0;i<N-1-i;i++)
if (m[i]>m[i+1]) {t=m[i];m[i]=m[i+1];m[i+1]=t;flag=1;}
}while(flag)
Обход дерева
struct Node
{
Node *parent,*left,*right;
};
void Action(Node *node)
{
if (node == NULL) return;
//action;
Action(node->left);
Action(node->right);
}
void Action2(Node *node)
{
queue<Node*> q;
q.push(node);
do
{
node = q.front();
q.pop();
//action
if (node->left!=NULL) q.push(node->left);
if (node->right!=NULL) q.push(node->right);
}
while(!q.empty)
}
- Иванова Г.С. Технология программирования: Учебник для вузов. – М.: МГТУ им. Н.Э.Баумана, 2002.
- Подбельский В.В. Язык С++: Учебн. пособие. – М.: Финансы и статистика, 1995.
- Г. Майерс. Надёжность программного обеспечения. 1976 // Перев. на русский язык под ред. И.А.Махован и др. – М.: Мир, 1980.
- В. В. Шураков. Надежность программного обеспечения систем обработки данных: учеб. для вузов. Изд. 2-е, пеpеpаб. и доп. — М.: Финансы и статистика, 1987.— 272 с
- Электронная энциклопедия ru.wikipedia.org
[1] https://ru.wikipedia.org/wiki/C
[2] Квадратные скобки не являются частью записи формата, а указывают на необязательность аргумента
Рабочий журнал воспитателя ДОУ (Белая К.Ю., Кондрыкинская Л.А. М.: ТЦ Сфера, 2012)
Наличие 4-х разделов плана:
I раздел. Общие сведения (в таблицах)
• сведения о детях и родителях;
• взаимодействие с семьями детей;
• режим дня группы (холодный период года);
• режим дня группы (теплый период года);
• листок здоровья;
• система закаливания в группе;
• двигательный режим;
• гимнастика;
• результаты обследования речи детей;
• индивидуальная работа с детьми по звуковой культуре речи.
II раздел. Комплексно-тематическое планирование психолого-педагогической работы с детьми
Это планирование на месяц и недели с выбором тем. Схема включает следующие 6 разделов:
• месяц (разделен на недели);
• события, праздники, традиции;
• тема;
• организация развивающей среды для самостоятельной деятельности детей;
• формы организации совместной деятельности педагогов с детьми;
• взаимодействие с семьей.
III раздел. Перспективное планирование по видам детской деятельности
Представлено в таблицах на месяц. Каждая таблица имеет свою специфику, что является хорошей подсказкой воспитателю.
• двигательная;
• игровая;
• коммуникативная;
• трудовая;
• познавательно-исследовательская;
• продуктивная;
• музыкально-художественная;
• чтение.
IV раздел. Планирование непосредственно-образовательной деятельности (НОД)
Первый лист – Расписание НОД на I и II полугодия.
Последующие листы оформлены как еженедельный план работы, включающий два блока: содержание НОД и формы организации детей.
Приложение 4. Карта развития ребенка по Васильевой М.А.
Карта развития ребёнка 6-7 лет (по Программе под ред. М.А. Васильевой)
| ОБРАЗОВАТЕЛЬНЫЕ ОБЛАСТИ | ИТОГОВЫЕ РЕЗУЛЬТАТЫ | ||
| 1. Физическое направление | Здоровье | 1. Усвоены основные культурно-гигиенические навыки (при умывании, пользовании индивидуальными принадлежностями, пользовании вещами). 2. Имеет сформированные представления о ЗОЖ (особенностях строения и функциях организма человека, соблюдении режима дня, рациональном питании, значении активности в жизни человека, т.д.). | |
| Физическая культура | 1. Выполняет правильно все виды основных движений (ходьба, бег, прыжки, метание, лазание). 2. Сформированы основные физические качества (быстрота, ловкость, гибкость, сила, т.д.) 3. Выполняет физические упражнения из разных исходных положений, чётко и ритмично, в заданном темпе, под музыку, по словам. Выполняет перестроения в 3-4 колонны, в 2-3 круга на ходу, в 2-3 шеренги. 4. Следит за правильной осанкой. 5. Участвует в играх с элементами спорта (городки, бадминтон, футбол, хоккей, настольный теннис). | ||
| 2. Познавательно- речевое направление | Познание | Продуктивная (конструктивная) деятельность | 1. Способен соотносить конструкцию предмета с его назначением. 2. Способен создавать различные конструкции одного и того же объекта. 3. Может создавать модели из разного вида конструкторов по рисунку и словесной инструкции. |
| ФЭМП | 1. Самостоятельно объединяет различные группы предметов, имеющие общий признак, в единое множество и удаляет из множества отдельные элементы. Устанавливает соотношение между целым и частью; находит части целого и целое по частям. 2. Количественный порядковый счёт до 10 и дальше, начиная с любого числа. 3. Соотносит цифру (0-9) и количество предметов. 4. Составляет и решает задачи в одно действие на сложение и вычитание, оперируя цифрами и арифметическими знаками (+, -, =). 5. Различает величины: длину (ширину, высоту), объём (вместимость), знает способы измерения (измеряет длину предметов, отрезки прямых линий, объёмы жидких, сыпучих веществ с помощью условных мер). Понимает зависимость мерой и числом (результатом измерения). 6. Умеет делить предметы (фигуры) на несколько равных частей; сравнивать предмет и его часть. 7. Различает, называет: отрезок, угол, круг (овал), многоугольники (3-х, 4-х, 5-иугольники и др.), шар, куб. 8. Ориентируется в окружающем пространстве, на плоскости (лист, поверхность стола, т.д.), обозначает взаимное расположение, изменение движения объектов; пользуется знаковыми обозначениями). 9. Может определять временные отношения (день-неделя-месяц); время с точностью до 1 часа. 10. Знает состав чисел первого десятка (из отдельных единиц) и состав чисел первого пятка из двух меньших. Может получать каждое число первого десятка, прибавляя к предыдущему и вычитая единицу из следующего за ним в ряду. 11. Знает монеты достоинством 1, 5, 10 копеек; 1, 2, 5 рублей. 12. Знает название текущего месяца года; последовательность всех дней и времён года. | ||
| Формирование целостной картины мира | 1. Имеет разнообразные впечатления о предметах окружающего мира. Группирует предметы в соответствии с познавательной задачей. 2. Знает герб, флаг, гимн России, главный город страны. 3. Имеет представление о родном крае; его достопримечательностях. 4. Имеет представления о школе, библиотеке. 5. Знает некоторых представителях животного мира (звери, птицы, пресмыкающиеся, земноводные, насекомые). 6. Знает характерные признаки времён года и соотносит с каждым сезоном особенности жизни людей, животных, растений. 7. Знает правила поведения в природе и соблюдает их. 8. Устанавливает элементарные причинно-следственные связи с природными явлениями. | ||
| Коммуникация | 1. Пересказывает и драматизирует небольшие литературные произведения; составляет по плану и образцу рассказы о предмете, по сюжетной картинке, набору картин с фабульным развитием действия. 2. Употребляет в речи синонимы, антонимы, сложные предложения разных видов. 3. Различает понятия «звук», «слог», «слово», «предложение». Называет в последовательности слова в предложении, звуки и слоги в словах, находит слова с заданным звуком, определяет место звука в слове. | ||
| Чтение художественной литературы | 1. Проявляет активный интерес к чтению как процессу. 2. Различает жанры литературных произведений. 3. Называет любимые сказки и рассказы; знает наизусть 2-3 стихотворения, 2-3 считалки, 2-3 загадки. 4. Называет 2-3 авторов и 2-3 иллюстраторов книг. 5. Выразительно читает стихотворение, пересказывает отрывок из рассказа. | ||
| 3.Социально- личностное развитие | Социализация | 1. Самостоятельно отбирает или придумывает разнообразные сюжеты игр. 2. Придерживается в процессе игры намеченного замысла, оставляя место для импровизации. Находит новую трактовку роли и исполняет её. 3. Может моделировать предметно-игровую среду. 4. В дидактических играх договаривается со сверстниками об очерёдности ходов, выборе схем; проявляет себя терпимым и доброжелательным партнёром. 5. Понимает образный строй спектакля: оценивает игру актёров, средств выразительности и оформление постановки. 6. В беседе о просмотренном спектакле может высказать свою точку зрения. 7. Владеет навыками театральной культуры: знает театральные профессии, правила поведения в театре. 8. Участвует в творческих группах по созданию спектакля («режиссёры», «актёры», «костюмеры», «оформители» и т.д.). | |
| Труд | 1. Самостоятельно ухаживает за одеждой, устраняет непорядок в своём внешнем виде. 2. Ответственно выполняет обязанности дежурного по столовой, в уголке природы. 3. Проявляет трудолюбие в работе на участке детского сада. 4. Избирательно освоил некоторые виды ручного труда. 5. Может планировать свою трудовую деятельность; отбирать материалы необходимые для занятий, игр. | ||
| Безопасность | 1. Соблюдает элементарные правила организованного поведения в детском саду, поведения на улице, дорожного движения. 2. Различает и называет специальные виды транспорта («Скорая помощь», «Пожарная», т.д.), объясняет их назначение. 3. Понимает значения сигналов светофора, узнаёт и называет дорожные знаки «Пешеходный переход», «Дети», «Остановка общественного транспорта», «Подземный пешеходный переход», «Пункт медицинской помощи». 4. Различает проезжую часть, тротуар, подземный пешеходный переход, пешеходный переход «Зебра». 5. Знает и соблюдает элементарные правила поведения в природе (способы безопасного взаимодействия с растениями и животными, бережного отношения к окружающей среде). | ||
| 4. Художественно-эстетическое направление | Музыка | 1. Определяет жанр прослушанного произведения (марш, песня, танец), инструмент, на котором оно исполняется. 2. Определяет общее настроение, характер музыкального произведения. 3. Различает части музыкального произведения (вступление, заключение, запев, припев). 4. Может петь песни в удобном диапазоне, индивидуально и коллективно, с сопровождением и без него, исполняя их выразительно, правильно передавая мелодию (ускоряя, замедляя, усиливая и ослабляя звучание). 5. Умеет выразительно и ритмично двигаться в соответствии с разнообразным характером музыки, музыкальными образами; передавать несложный музыкальный ритмический рисунок. 6. Умеет выполнять танцевальные движения (шаг с притопом, приставной шаг с приседанием, пружинящий шаг, боковой галоп, переменный шаг). 7. Инсценирует игровые песни, придумывает варианты образных движений в играх и хороводах. 8. Исполняет сольно и в ансамбле на ударных и звуковысотных детских музыкальных инструментах несложные песни и мелодии. | |
| Художественное творчество | 1. Различает виды изобразительного искусства: живопись, графика, скульптура, декоративно-прикладное и народное искусство. Называет основные выразительные средства произведений искусства. 2. Создаёт индивидуальные и коллективные рисунки, предметные и сюжетные композиции на темы окружающей жизни, литературных произведений. 3. Использует разные материалы и способы создания изображения. 4. Лепит различные предметы, передавая их форму, пропорции, позы и движения; создаёт сюжетные композиции из 2-3 и более изображений. 5. Выполняет декоративные композиции способами налепа и рельефа. Расписывает вылепленные изделия по мотивам народного искусства. 6. Создаёт изображения различных предметов, используя бумагу разной фактуры и способы вырезания и обрывания. 7. Создаёт сюжетные и декоративные композиции. |
Приложение 4. Темы рефератов:
1. «Активные формы методической работы в ДОУ».
1. Написать реферат на одну из предложенных тем:
• Стили руководства в ДОУ.
• Выработка индивидуального стиля деятельности как один из путей самовыражения руководителя.
• Причины и виды конфликтов в коллективе. Пути и способы предупреждения конфликтов.
Влияние личности руководителя на социально-психологический климат в коллективе.
[1] * - материал для самостоятельного изучения
Экономико-математическая модель
межотраслевого баланса «затраты-выпуск»
1. Модель «затраты-выпуск». Открытая модель Леонтьева.
- Общая структура статического межотраслевого баланса (МОБ).
- Модель межотраслевого баланса затрат труда
- Матричные модели предприятий, фирм.
Эффективное ведение народного хозяйства предполагает наличие баланса (равенства) между отдельными отраслями экономической системы. Межотраслевой баланс в экономике – это метод анализа взаимосвязей между различными секторами экономической системы.
Цель балансового анализа – определить, сколько продукции должна произвести каждая отрасль для того, чтобы удовлетворить все потребности экономической системы.
Пусть экономическую систему можно разделить на несколько отраслей, производящих определенные товары и услуги. При производстве товаров и услуг в каждой отрасли расходуются определенные ресурсы, которые производятся как в других отраслях, так и в данной отрасли. То есть каждая отрасль экономики выступает в системе межотраслевых связей, с одной стороны, как производитель некоторой продукции, а с другой – как потребитель продукции, вырабатываемой другими отраслями. Для наглядности выражения взаимной связи между отраслями пользуются так называемыми таблицами межотраслевого баланса.
Математическую модель межотраслевого баланса предложил американский экономист В.В. Леонтьева (в 1936 г.). За ее разработку и применение к решению экономических проблем в 1973г. он был удостоен Нобелевской премии в области экономики. В западной литературе модели данного класса именуются как метод «затраты-выпуск». [i]
- Модель «затраты-выпуск». Открытая модель Леонтьева.
Рассмотрим открытую модель межотраслевого баланса, в которой вся произведенная продукция (валовой продукт) разделяется на две части: одна часть идет на потребление в производящих отраслях, а другая часть (конечный продукт) потребляется вне сферы материального производства – в секторе конечного спроса, при этом потребление может меняться.
Пусть вся экономика страны представляется в виде n отраслей, взаимодействующих между собой. Рассматривается некоторый определённый промежуток времени [T0, T1], обычно - это процесс производства за один год.
Введём следующие обозначения.
Пусть Xi – общий объём продукции отрасли i за данный промежуток времени – так называемый валовой выпуск отрасли i;
xij – объём продукции отрасли i, потребляемой отраслью j в процессе производства;
yi – объём конечной продукции отрасли i для непроизводственного, конечного потребления. Этот объём составляет обычно более 75% всей произведённой продукции. В него входят: создаваемые в хозяйстве запасы, личное потребление граждан, обеспечение общественных потребностей (просвещение, наука, здравоохранение, развитие инфраструктуры и т.д.), поставки на экспорт. Указанные величины можно свести в таблицу.
| Отрасли производители | потребители 1 2 …. n | Конечный продукт | Валовой выпуск |
| Отрасль 1 Отрасль 2 … Отрасль n | x11 x12.....x1n x21 x22...x2n ........ I........... xn1 xn2 ...xnn | y1 y2 .. II.. yn | Х1 Х2 ... Хn |
Раздел (квадрант) I – содержит информацию о межотраслевых связях. Величины xij характеризуют межотраслевые поставки сырья, материалов, топлива и др, обусловленные производственной деятельностью.
В i-той строке величины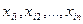 
показывают распределение продукции i-той отрасли как средства производства для других отраслей.
В столбце j величины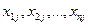 
показывают потребление j-той отраслью продукции других отраслей в процессе производства (расходы).
Балансовый характер этой таблицы выражается в том, что при любом i = 1,...,n должно выполняться соотношение (равенство–баланс):
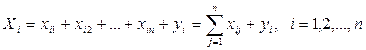(1) – уравнение баланса
В нормально функционирующей экономике должен быть сбалансирован объём, производимой отраслями продукции, и внутриотраслевое потребление вместе с конечным потреблением (свободный рынок). Уравнение (1) называют уравнением баланса.
Уравнение баланса содержит две неизвестные величины Xi и xij и одну известную – конечное потребление yi и, следовательно, уравнение (1) не имеет единственного решения, и поэтому не может быть использовано для моделирования процессов сбалансированности процессов производства и потребления.
В. Леонтьев, рассматривая развитие американской экономики в предвоенный период, заметил, что величина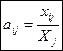 
, сохраняет ≈ постоянное значение в течение нескольких лет, что связано с технологиями производства, которые меняются сравнительно медленно. Поэтому можно считать, что aij = const.
Экономический смысл aij: коэффициент aij показывает затраты продукции отрасли i на единицу валовой продукции отрасли j, с учетом только прямых затрат.
Следовательно, для выпуска любого объёма Xj продукции отрасли j необходимо затратить продукцию отрасли i в количестве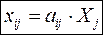 
(2).
Коэффициенты aij называют коэффициентами прямых затрат.
Матрицу, этих коэффициентов – матрицей прямых затрат.
Соотношение (1) принимает вид:
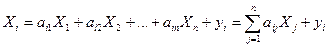или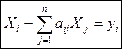 
, где i=1,2,…,n (3)
Экономический смысл**: равенства (3) описывают технологию производства и структуру экономических связей и означают, что в конечное потребление от каждой производящей отрасли поступает та часть произведенной продукции, которая остается после того, как обеспечены потребности производящих секторов.
Каждое из уравнений (3) уже содержит одну неизвестную Х i, и поэтому оно может быть использовано для моделирования (планирования) процессов производства и потребления.
Рассмотрим матрично-векторное описание поставленной задачи. Введем обозначения: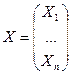 
– вектор валового выпуска, 
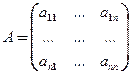– матрица прямых затрат (структурная матрица), 
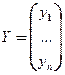– вектор конечного продукта, тогда уравнение (3) можно записать в матричном виде: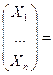 
+
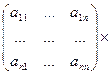
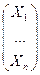Или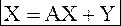 
(4) – уравнение линейного межотраслевого баланса
Соотношение (4) называют уравнением линейного межотраслевого баланса (МОБ), или открытой балансовой моделью Леонтьева или моделью «затраты-выпуск».
Следовательно, балансовая модель это система уравнений, каждое из которых выражает требование баланса (равенства) между количеством продукции, производимым отдельными отраслями экономической системы и совокупной потребностью в этой продукции.
Линейную балансовую модель называют открытой, если вся произведенная продукция системы разделяется на 2 части: одна часть идет на потребление в производящих отраслях, а другая - (конечный продукт) потребляется вне сферы материального производства Х=АХ+Y
Линейная балансовая модель называется закрытой, если вся продукция системы затрачивается внутри системы Х=АХ.
Все компоненты матрицы A, вектора X и вектора Y должны быть неотрицательны (это вытекает из экономического смысла A, Х и Y). Для краткости, неотрицательность элементов матрицы A и векторов Х и Y, будем записывать так: A≥0, Х≥0, Y≥0.
