Пример 1. В таблице данные об исполнении баланса за отчетный период.
| Отрасли | Потребление | Конечный продукт | Валовой выпуск | ||
| Энергетика | Машиностроение | ||||
| производство | Энергетика | ||||
| Машиностроение |
Найти:
1) вектор валовой продукции.
2) Матрицу А коэффициентов прямых производственных затрат.
3) Проверить продуктивность матрицы А
4) Найти матрицу коэффициентов полных производственных затрат.
5) Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление энергетики увеличится вдвое, а машиностроение останется на прежнем уровне.
Решение:
1)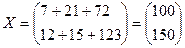
Следовательно: 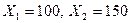
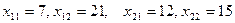
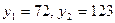
2) Найдем коэффициенты прямых затрат по формуле 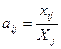
i=1, j=1: 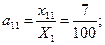 i=1, j=2:
i=1, j=2: 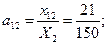
i=2, j=1: 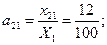 i=2, j=2:
i=2, j=2: 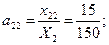 Þ
Þ 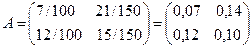
3) Матрица А продуктивная, следовательно для любого вектора конечного продукта Y можно найти необходимый объем валового выпуска Х по формуле: 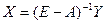
4) Найдем матрицу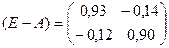 ;
; 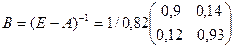
5) По условию вектор 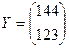 ;
; 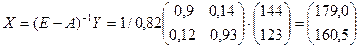
Ответ: валовой выпуск в энергетике надо увеличить до 179 усл.ед, а в машиностроении до 160,5 усл.ед
Пример 2. (А.В. Идельсон стр. 171 пример 3.)
Система состоит из двух отраслей.
Дана матрица прямых производственных затрат 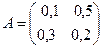 .
.
Требуется:
1) Проверить продуктивность матрицы А.
2) найти вектор валовой продукции Х, необходимый для того, чтобы обеспечить выпуск конечной продукции Y=(400, 500).
3) Приращение вектора валовой продукции, необходимое для увеличения выпуска конечной продукции соответственно на DY=(100, 50)
Решение.
1. Проверить продуктивность матрицы А.
2. Найти матрицу полных производственных затрат.
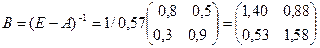
3. Вычислить 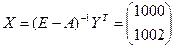 , т.е. чтобы обеспечить выпуск на внешнее потребление 400 ед. продукции 1-й и 500 ед. продукции 2-й отрасли, первая отрасль должна произвести 1000 ед., а вторая 1002 ед. продукции.
, т.е. чтобы обеспечить выпуск на внешнее потребление 400 ед. продукции 1-й и 500 ед. продукции 2-й отрасли, первая отрасль должна произвести 1000 ед., а вторая 1002 ед. продукции.
4. Найти новый вектор 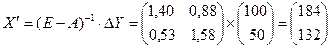
Валовая продукция 1-й отрасли д.б. увеличена ни 184 ед., а 2-й – на 132 ед.
Пример 3. (31) Пусть дана балансовая модель Даны матрица прямых затрат и вектор валовой продукции. Найти вектор конечной продукции Y. 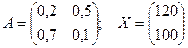
Пример 4. Дана модель “затраты-выпуск”. Найти производственную программу цехов, т.е. х ij.
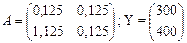
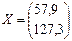
Домашнее задание 2.
 2014-02-09
2014-02-09 5385
5385








