Бескоалиционные игры

Рассмотрим бескоалиционную игру, когда каждый игрок действует самостоятельно. Пусть 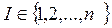— множество игроков. Каждый из игроков имеет некоторое множество 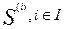своих стратегий. Число стратегий образует множество стратегий каждого игрока, и это число должно быть не меньше двух.

Процесс игры состоит в выборе каждым игроком своей стратегии 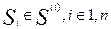. В результате этого выбора определяется исход партии: 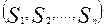. Пусть 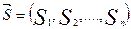— вектор ситуаций в игре, тогда 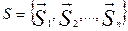— множество всех ситуаций в игре. С другой стороны, множество всевозможных ситуаций S можно рассматривать как . Выигрыш каждого игрока в каждой ситуации определяется следующим выражением: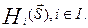

Тогда после всех введенных обозначений бескоалиционной игрой называют систему следующего вида:

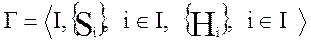
В бескоалиционной игре все множества являются множествами вещественных чисел. Среди явлений, описываемых посредством бескоалиционных игр, довольно много таких, когда по результатам игры приходится распределять некоторые ресурсы.

В теории игр также выделяют игры с постоянной суммой: бескоалиционная игра называется игрой с постоянной суммой, если существует такая константа c, что выполнятся условие 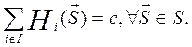Если 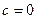, то бескоалиционная игра называется игрой с нулевой суммой.