Правило последовательных выборок

Выборка — результаты испытаний.

Пусть выделены каким-либо образом области останова: .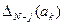

Правило последовательных выборок состоит в следующем:

Первоначально известно априорное состояние природы 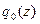, 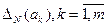. В запасе все N экспериментов. Если 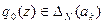, то принимаем решение 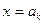. Если 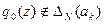, то принимается решение провести первый эксперимент. Проведя первое испытание, рассчитывается ,

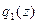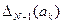
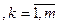
а) Если 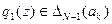то принимают решение .

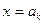б) Если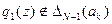то принимают решение продолжить эксперимент, j=2 и т.д., до тех пор пока j=N.

Если для всех N-1 наблюдений выполняется условие типа «б», то проводят последнее испытание, после которого выбор решения уже обязателен.

Очевидно,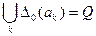, где Q — множество смешанных стратегий природы. Отсюда видно, что задача определяется последовательностью 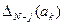для всех j=1,2,...,N.