Детерминированных сигналов

Наряду со спектральным подходом к описанию сигналов часто на практике оказывается необходимым характеристика, которая давала бы представление о некоторых свойствах сигнала, в частности о скорости изменения во времени, а также о длительности сигнала без разложения его на гармонические составляющие.

В качестве такой временной характеристики широко используется Корреляционная функция сигнала.

Для детерминированного сигнала S(t) конечной длительности корреляционная функция определяется следующими выражениями:

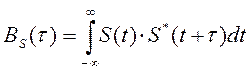
(2.128)

где 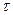- временной сдвиг сигнала.

{ Здесь мы будем рассматривать сигналы, являющиеся вещественными функциями времени, и в этой связи обозначение комплексного сопряжения можно опустить: }

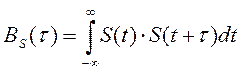(2.129)

Из (.129) видно, что 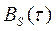характеризует степень связи (корреляции) сигнала S(t) со своей копией, сдвинутой на величину 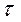по оси времени. Ясно, что функция 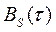достигает максимума при 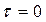, так как любой сигнал полностью коррелирован с самим собой. При этом

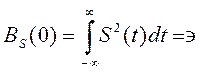(2.130)

Т.е максимальное значение авто - корреляционной функции равно энергии сигнала.

С увеличением 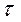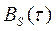убывает (не обязательно монотонно) и при относительном сдвиге сигналов S(t) и 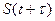на время, превышающее длительность сигнала, обращается в нуль.

На рисунке 2.36 показано построение корреляционной функции для простейшего сигнала в виде прямоугольного импульса (рис. 2.36.а). Сдвинутый на 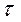на рис. 2.36-б,а произведение 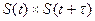- на рис. 2.36-в. График функции 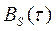изображен на рис. 2.36,2. Каждому значению 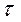соответствует своё произведение 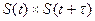и площадь под графиком функции 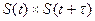. Численные значения таких площадей для соответствующих 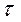и дают ординаты функций .

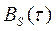Аналогичное построение для треугольного импульса изображено на рис. 2.37. Из общего определения корреляционной функции, а так же из приведённых примеров видно, что безразлично, вправо или влево относительно своей копии сдвигать сигнал на величину 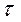. Поэтому выражение (2.129) можно обобщить следующим образом:

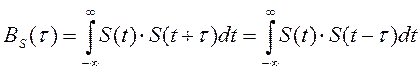(2.129’)

Это равносильно утверждению, что 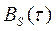является чётной функцией 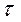нарис. 2.38-а показан сигнал в виде пачки из 4-х одинаковых импульсов, сдвинутых один относительно другого на время 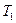, а на рис. 2.38-б – соответствующая этому сигналу корреляционная функция. Вблизи значений 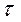, равных 0, 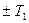, 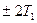и 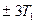, эта функция имеет такой же вид, как и для одиночного импульса (см. рис. 2.36-2).

Максимальное значение корреляционной функции (при ) равно учетверённой энергии одного импульса.

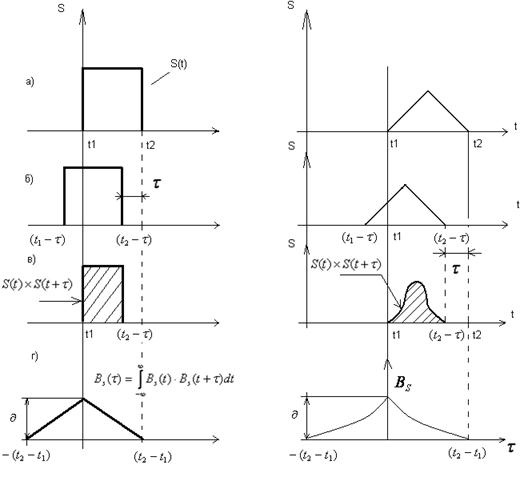
Рис. 2.36 рис. 2.37 Построение корреляци-

Построение корреляционной оной функции для треугольного

функции для прямоугольного импульса.

импульса.

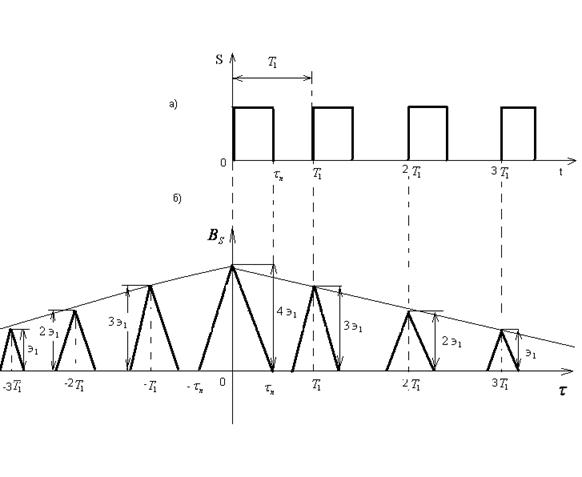
Рис. 2.38. Пачка из 4-х прямоугольных импульсов (а) и корреляционная функция этой пачки (б).

Для периодического сигнала, энергия которого бесконечно велика, определение корреляционной функции с помощью выражений (2.129) или (2.129’) не приемлемо. В этом случае исходят из следующего определения:

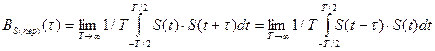(2.131)

При таком определении корреляционная функция приобретает размерность мощности, причем 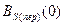равна средней мощности периодического сигнала.

Ввиду периодичности сигнала S(t) усреднение произведения 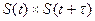или 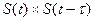по бесконечно большому отрезку T должно совпадать с усреднением по периоду 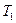. Поэтому выражение (2.131) можно заменить выражением:

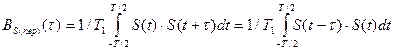(2.132)

Входящие в это выражение интегралы есть не что иное, как корреляционнаяфункция сигнала на интервале 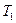. Обозначая её через 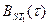, приходим к соотношению:

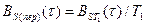
Очевидно, что периодическому сигналу S(t) соответствует и периодическая корреляционная функция 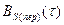. Период функции 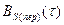совпадает с периодом 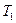исходного сигнала S(t).

Например, для простейшего (гармонического) колебания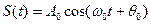

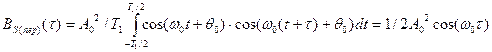
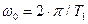
Корреляционная функция

При 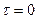, 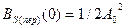-есть средняя мощность гармонического колебания с амплитудой .

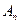Важно отметить, что корреляционная функция 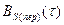не зависит от начальной фазы колебания .

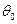На (рис. 2.39-б) изображена корреляционная функция сигнала, представляющего собой периодическую последовательность прямоугольных импульсов (рис. 2.39-а).

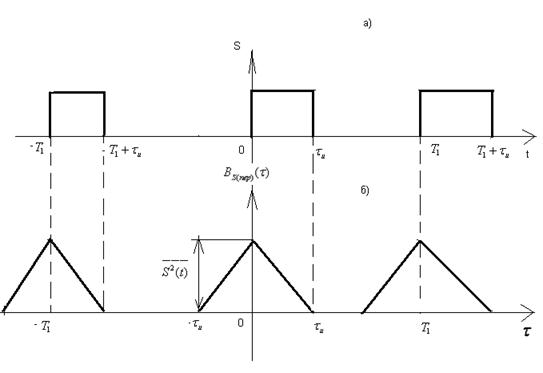
Рис. 2.39. Периодическая последовательность импульсов (а) и её корреляционная функция (б).

Каждый из импульсов функции 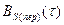совпадает по форме с корреляционной функцией одиночного импульса из периодической последовательности S(t). Однако в данном случае максимальные ординаты 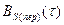равны не энергии (как на рис. 2.38), а средней мощности сигнала S(t), т.е величине .

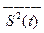Для оценки степени связи между двумя различными сигналам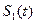и и 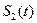используется взаимная корреляционная функция, определяемая общим выражением:

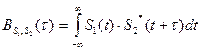(2.133)

Для вещественных функци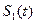й и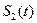

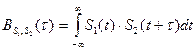(2.134)

Рассмотренная выше корреляционная функция 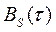является частным случаем функции 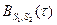, когда .

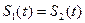Построение взаимной корреляционной функции для двух сигналов 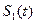и 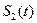приведено на рис.2-40. Исходное положение сигнала 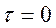показано (на рис. 2.40-а). При сдвиге сигнала 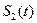влево (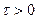, рис. 2.40-б) корреляционная функция сначала возрастает, а затем убывает до нуля при .

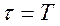При сдвиге вправо (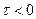) корреляционная функция сразу убывает. В результате получается ассиметричная относительно оси ординат функция 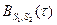(рис. 2.40-в).

Очевидно, что значение 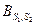не изменится, если вместо упреждения сигнала 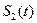дать задержку сигналу .

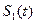Поэтому (2.134) можно обобщить следующим образом:

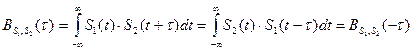(2.135)

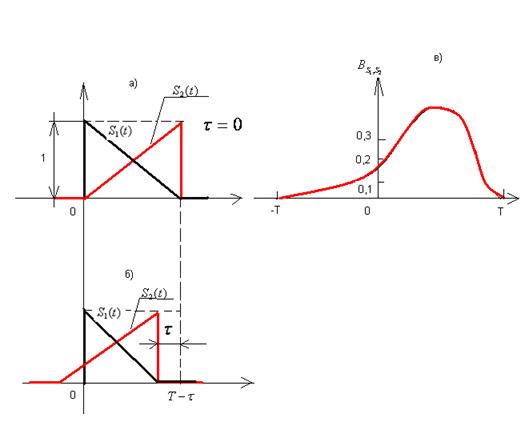
Рис. 2.40 Построение взаимной корреляционной функции:

а) исходное положение сигналов;

б) сдвиг сигнал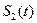а на 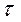влево;

в) взаимная корреляционная функция.

Соответственно

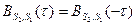(2.135’)

Следует, однако, различать (2.129’) и (2.135’).

В отличие от 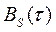взаимная корреляционная функция не обязательно является чётной относительно 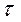. Кроме того, взаимная корреляционная функция не обязательно достигает максимума при 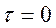. Оба этих свойства взаимной корреляционной функции иллюстрируются на рис.2.40.