Воспользуемся выражением для интеграла от произведения 2-х функций.
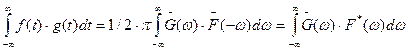 (2.63)
(2.63)
В (2.63) положим f(t)=S(t), а 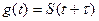 и, соответственно
и, соответственно 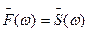 ; а
; а 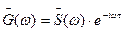 , тогда получим:
, тогда получим:
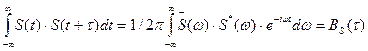
Учитывая, что 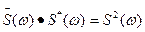 , приходим к искомой зависимости
, приходим к искомой зависимости
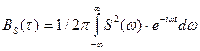 (2.136)
(2.136)
На основании известных свойств преобразований Фурье можно также написать:

 (2.137)
(2.137)
{Вследствие чётности функции 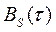 знак перед
знак перед 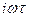 в показателе степени м.б. произвольным. То же относится к 2.137.}
в показателе степени м.б. произвольным. То же относится к 2.137.}
Итак, прямое преобразование Фурье (2.137) корреляционной функции 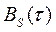 дает спектральную плотность энергии, а преобразование (2.136) дает корреляционную функцию
дает спектральную плотность энергии, а преобразование (2.136) дает корреляционную функцию 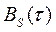 . Из (2.136) и (2.137) вытекают следующие свойства:
. Из (2.136) и (2.137) вытекают следующие свойства:
1.) Чем шире спектр сигнала 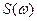 , тем меньше интервал корреляции, т.е. сдвиг
, тем меньше интервал корреляции, т.е. сдвиг 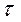 , в пределах которого корреляционная функция отличена от нуля.
, в пределах которого корреляционная функция отличена от нуля.
2.) Соответственно: Чем больше интервал корреляции заданного сигнала, тем уже его спектр.
Из (2.136) и (2.137) видно также, что корреляционная функция 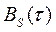 не зависим от ФЧХ спектра сигнала. Так как при заданном амплитудном спектре
не зависим от ФЧХ спектра сигнала. Так как при заданном амплитудном спектре 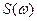 форма функции S(t) существенно зависит от ФЧХ, то можем сделать следующее заключение:
форма функции S(t) существенно зависит от ФЧХ, то можем сделать следующее заключение:
3.) различным по форме сигналам S(t), обладающим одинаковыми амплитудными спектрами, соответствуют одинаковые корреляционные функции 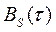 .
.
 2014-02-10
2014-02-10 879
879







