Уравнение Лапласа в координатах 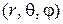 записывается так:
записывается так:
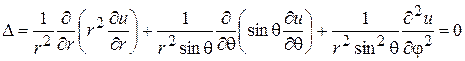 . (1)
. (1)
Следуя методу Фурье, ищем решение этого уравнения в виде произведения:
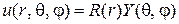 . (2)
. (2)
Подставляя (2) в (1), получаем:
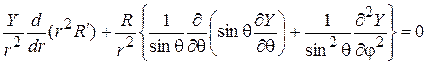 .
.
Умножим это равенство на 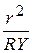 , приводим его к виду:
, приводим его к виду:
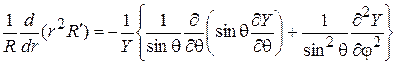 . (3)
. (3)
Приравнивая обе части равенства (3) постоянной l, приходим к двум уравнениям:
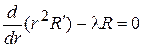 , (4)
, (4)
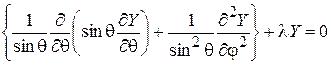 . (5)
. (5)
Как видим, уравнение (5) есть уравнение в частных производных. Поэтому вновь применим метод Фурье.
Представим 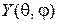 в виде произведения:
в виде произведения:
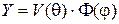 (6)
(6)
и подставим это выражение в (5). Тогда
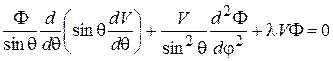 .
.
Умножим последнее равенство на 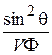 и разделив переменные, приходим к равенству:
и разделив переменные, приходим к равенству:
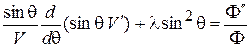 .
.
Приравнивая обе части постоянной 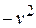 , получаем два обыкновенных дифференциальных уравнения:
, получаем два обыкновенных дифференциальных уравнения:
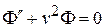 , (7)
, (7)
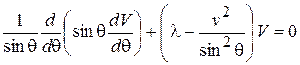 . (8)
. (8)
Решение уравнения (7) нам удобнее представить в показательной форме:
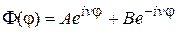 . (9)
. (9)
Так как обычно функция 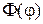 удовлетворяет условию цикличности
удовлетворяет условию цикличности
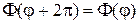 ,
,
то можно сделать вывод, что значение v не может быть произвольным, а обязательно является целочисленным 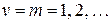 . Следовательно, функция
. Следовательно, функция 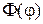 принимает форму:
принимает форму:
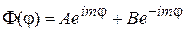 , (10)
, (10)
а уравнение (8) соответственно запишется так:
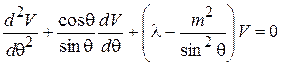 . (11)
. (11)
Уравнение (11) называют обобщенным уравнением Лежандра. Если ввести новую независимую переменную 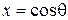 (при этом
(при этом 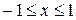 ) и обозначить
) и обозначить 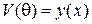 , то обобщенное уравнение Лежандра принимает обычный вид:
, то обобщенное уравнение Лежандра принимает обычный вид:
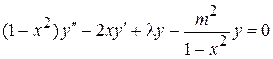 . (12)
. (12)
При 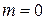 это уравнение имеет более простую форму уравнения Лежандра:
это уравнение имеет более простую форму уравнения Лежандра:
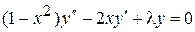 . (13)
. (13)
Таким образом, задача свелась к нахождению решений уравнения Лежандра (11) и уравнения Эйлера (4). Обозначая их интегралы соответственно через 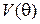 и
и  , представим искомую функцию в форме следующего произведения:
, представим искомую функцию в форме следующего произведения:
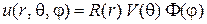 . (14)
. (14)
Решение уравнения Лежандра. Только при выполнении равенства 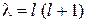 можно получит конечные решения уравнения Лежандра. Таким образом, удовлетворяющее условию уравнение Лежандра
можно получит конечные решения уравнения Лежандра. Таким образом, удовлетворяющее условию уравнение Лежандра

имеет ограниченное решение, которое представляет собой многочлен l -й степени. Ограниченные решения уравнения Лежандра могут существовать, только если 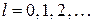 . При этом оказывается, что они являются полиномами
. При этом оказывается, что они являются полиномами  Лежандра.
Лежандра.
| l =0, | 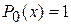 | 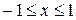 |
| l =1, | 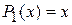 | 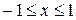 |
| l =2, | 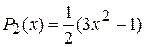 | 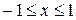 |
| l =3, | 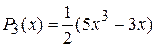 | 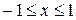 |
| … | … | … |
| l | 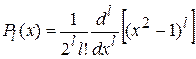 | 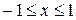 (формула Родрига) (формула Родрига) |
Конечными решениями обобщенного уравнения Лежандра (12) являются так называемые присоединенные полиномы Лежандра 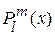 , определяемые следующей формулой Родриго:
, определяемые следующей формулой Родриго:
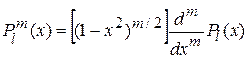 .
.
При 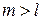 имеет место тождество
имеет место тождество 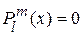 . Поэтому каждому значению l соответствует l +1 присоединенных полиномов Лежандра
. Поэтому каждому значению l соответствует l +1 присоединенных полиномов Лежандра
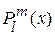 ,
,
где 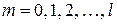 . Графики нескольких полиномов Лежандра изображены на рисунке 9.
. Графики нескольких полиномов Лежандра изображены на рисунке 9.


 |

P2
P3
 -1 1 x
-1 1 x
P1
-1
Рис. 9
Вернемся к исходной задаче. Поскольку уравнение (12) получилось из (11) заменой независимой переменной 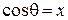 , то решение уравнения (11) имеет вид
, то решение уравнения (11) имеет вид
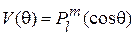 .
.
Осталось найти решение уравнения Эйлера (4). Так как нас интересует только конечные решения для всех внутренних точек шара (в том числе и центра, где 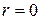 ), то
), то 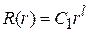 .
.
Следовательно, решение уравнения (1) имеет вид:
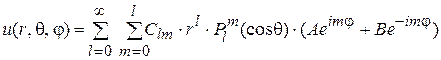 ,
,
коэффициенты 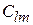 подбираются из граничных условий.
подбираются из граничных условий.
 2014-02-10
2014-02-10 5803
5803







