Л Е К Ц И И 15 - 17
Рис. 5.31. Спектральная характеристика лазера Рис. 5.32. Диаграммы направленности лазера
Наряду с пороговой плотностью тока важными параметрами лазера являются квантовый выход и КПД. Внешний квантовый выход определяется выражением (5.6).
Уравнение Лапласа в цилиндрических координатах имеет следующий вид:
 . (1)
. (1)
Будем искать решение уравнения (1) методом Фурье, имея в виду, что искомая функция  зависит от трех переменных.
зависит от трех переменных.
Положим, что
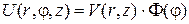 (2)
(2)
и подставим это произведение в (1). Тогда
 .
.
Если полученное равенство умножить на 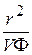 и член, зависящий от j, перенести вправо, то придем к равенству:
и член, зависящий от j, перенести вправо, то придем к равенству:
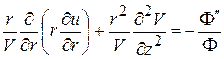 .
.
Но равенство двух функций от различных аргументов возможно тогда и только тогда, когда обе они равны одной и той же постоянной. Обозначая эту постоянную через 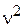 , получаем два уравнения:
, получаем два уравнения:
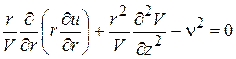 , (3)
, (3)
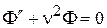 . (4)
. (4)
Поскольку (3) является уравнением в частных производных, то применим к нему метод Фурье с целью разделения переменных. Итак, пусть
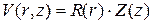 . (5)
. (5)
Деля (3) на 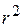 и подставляя в него (5), приходим опять к равенству:
и подставляя в него (5), приходим опять к равенству:
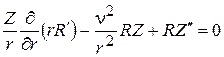 .
.
Делим далее на произведение RZ и переносим вправо член, зависящий от z:
 .
.
Мы получили равенство двух функций от различных аргументов. Приравнивая обе части этого равенства постоянной 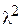 , получаем два обыкновенных дифференциальных уравнения:
, получаем два обыкновенных дифференциальных уравнения:
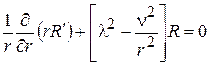 . (6)
. (6)
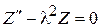 . (7)
. (7)
Ясно, что совокупность уравнений (4), (6) и (7) эквивалентна исходному уравнению Лапласа (1) и позволяет в принципе определить функции 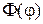 ,
,  ,
,  , а следовательно, и искомую функцию U, которая согласно (2) и (5) равна:
, а следовательно, и искомую функцию U, которая согласно (2) и (5) равна:
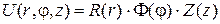 . (8)
. (8)
Поскольку дифференциальные уравнения (4) и (7) являются хорошо известными линейными и однородными уравнениями второго порядка, то их общие решения можно сразу же написать:
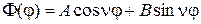 , (9)
, (9)
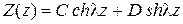 . (10)
. (10)
Таким образом, задача сводится к решению дифференциального уравнения (6) с переменными коэффициентами. Его, очевидно, можно представить, так:
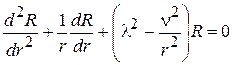 . (6а)
. (6а)
Если ввести новую независимую переменную  , то (6а) несколько упрощается и принимает форму так называемого уравнения Бесселя:
, то (6а) несколько упрощается и принимает форму так называемого уравнения Бесселя:
 . (11)
. (11)
Интегралы этого уравнения  называются цилиндрическими функциями или функциями Бесселя.
называются цилиндрическими функциями или функциями Бесселя.
Перейдем теперь к рассмотрению методов определения решения уравнения (11).
Решение уравнения Бесселя. Функции Бесселя. Запишем уравнение Бесселя в виде:
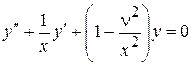 (12)
(12)
и будем искать его решение в форме ряда:
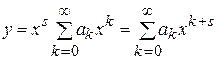 . (13)
. (13)
Первая и вторая производные этого ряда запишутся так:
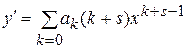 , (13а)
, (13а)
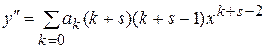 . (13б)
. (13б)
Умножим (13) на  и (13а) - на
и (13а) - на  и полученные выражения вместе с (13б) подставим в (12):
и полученные выражения вместе с (13б) подставим в (12):
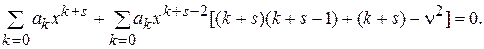
Произведя сокращение на  и упрощения в квадратных скобках, преобразуем это тождественное равенство следующим образом:
и упрощения в квадратных скобках, преобразуем это тождественное равенство следующим образом:
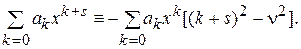
Ряд слева начинается с  , а ряд справа - с x в нулевой степени. Отсюда следует, что коэффициенты перед
, а ряд справа - с x в нулевой степени. Отсюда следует, что коэффициенты перед 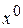 и
и 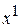 равны нулю:
равны нулю:
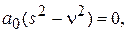 (14)
(14)
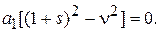 (14а)
(14а)
Что касается коэффициентов при более высоких степенях x, то они должны удовлетворять рекуррентному равенству:
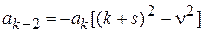 , (15)
, (15)
где k = 2, 3,.... Из (14) вытекает, что 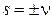 и
и 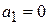 . Положим сначала, что
. Положим сначала, что 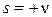 , тогда согласно (15)
, тогда согласно (15)
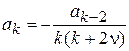 , (15а)
, (15а)
где k = 2, 3,.... Поскольку 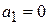 , то и все последующие нечетные коэффициенты
, то и все последующие нечетные коэффициенты  ,
, 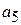 ,
,  ,... также равны нулю. Что касается четных коэффициентов, то их легко выразить через a по формуле (15а):
,... также равны нулю. Что касается четных коэффициентов, то их легко выразить через a по формуле (15а):
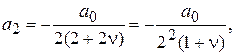
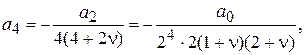
..................................
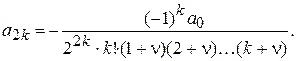 (16)
(16)
Подставляя (16) в (13), получаем частное решение уравнения Бесселя (12):
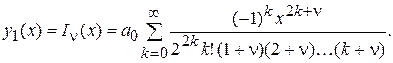 (17)
(17)
Ряд (17) сходится при любых значения x. Характеризуемая им функция 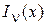 называется бесселевой функцией первого рода порядка n.
называется бесселевой функцией первого рода порядка n.
Бесселевы функции первого рода 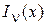 хорошо изучены, для них составлены таблицы. Для больших x кривая
хорошо изучены, для них составлены таблицы. Для больших x кривая 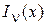 приблизительно представляет собой затухающую косинусоиду. На рисунке 7 приведен график бесселевой функции нулевого порядка.
приблизительно представляет собой затухающую косинусоиду. На рисунке 7 приведен график бесселевой функции нулевого порядка.
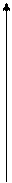

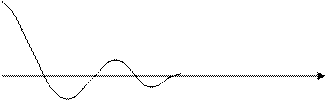 |
x
Рис. 7
Функция Бесселя первого рода 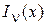 является одним частным решением
является одним частным решением 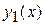 уравнения (12). Чтобы написать его общее решение, нужно знать второе линейно-независимое частное решение
уравнения (12). Чтобы написать его общее решение, нужно знать второе линейно-независимое частное решение 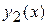 . В теории бесселевых функций показывается, что в том случае, когда параметр n является не целым числом, это второе частное решение можно получить, положив
. В теории бесселевых функций показывается, что в том случае, когда параметр n является не целым числом, это второе частное решение можно получить, положив 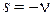 :
:
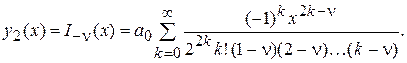 (18)
(18)
Это тоже бесселева функция первого рода, но отрицательного порядка, ее график подобен затухающей косинусоиде. В случае нецелочисленности n общий интеграл уравнения Бесселя имеет вид:
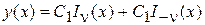 . (19)
. (19)
Однако, если n есть целое число (n = n), то функция 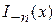 отличается от
отличается от 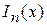 только постоянным множителем (-1). Иными словами,
только постоянным множителем (-1). Иными словами, 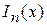 и
и 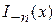 линейно зависимы и из них общий интеграл нельзя составить. В этом случае в качестве второго независимого частного решения выбирают функцию Бесселя второго рода
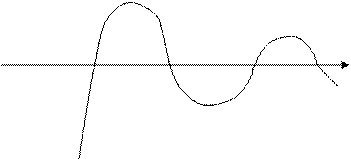
линейно зависимы и из них общий интеграл нельзя составить. В этом случае в качестве второго независимого частного решения выбирают функцию Бесселя второго рода 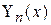 , которую еще называют функцией Неймана. Наиболее существенное свойство функции Неймана состоит в том, что при
, которую еще называют функцией Неймана. Наиболее существенное свойство функции Неймана состоит в том, что при 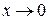 функция Неймана любого порядка стремится к бесконечности (рис. 7).
функция Неймана любого порядка стремится к бесконечности (рис. 7).
Таким образом, при n = n общий интеграл уравнения Бесселя (12) выражается следующей формулой:
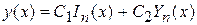 . (20)
. (20)

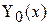
 |
x
Рис. 8
 2014-02-10
2014-02-10 5298
5298