Вблизи поверхности раздела двух диэлектриков векторы 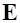 и
и 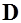 должны удовлетворять определенным граничным условиям. Рассмотрим плоскую границу раздела двух однородных диэлектриков с проницаемостями
должны удовлетворять определенным граничным условиям. Рассмотрим плоскую границу раздела двух однородных диэлектриков с проницаемостями 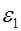 и
и 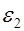 (см. рис. 3.5).
(см. рис. 3.5).
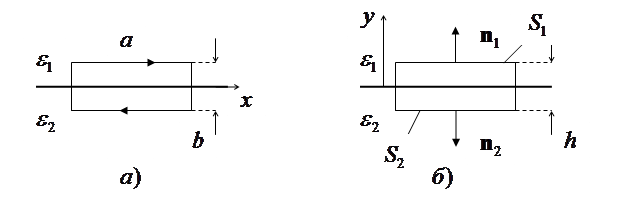

Рис. 3.5. К расчету граничных условий
Для замкнутого контура малого размера в окрестности границы раздела (рис. 3.5, а) применим условие потенциальности электрического поля
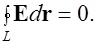
Стягивая контур к границе раздела (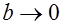 ), имеем:
), имеем:
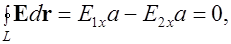
откуда следует 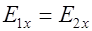 .
.
Вывод: При переходе через границу раздела двух диэлектриков касательная к этой границе компонента напряженности электрического поля не изменяется:
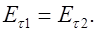 (3.18)
(3.18)
Для цилиндра малого размера в окрестности границы раздела (рис. 3.5, б) применим теорему Гаусса (3.17). Стягивая цилиндр к границе раздела (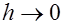 ), имеем:
), имеем: 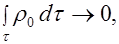 так как
так как 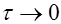 , тогда
, тогда
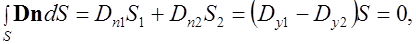
где 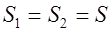 , откуда
, откуда 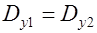 .
.
Вывод: При переходе через границу раздела двух диэлектриков нормальная к этой границе компонента индукции электрического поля не изменяется:
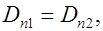 (3.19)
(3.19)
где под нормальной компонентой понимается проекция на одну и ту же нормаль 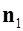 .
.
С учетом (3.13) из (3.18) и (3.19) найдем соотношения, описывающие изменение касательной компоненты индукции и нормальной компоненты напряженности поля при переходе через границу раздела:
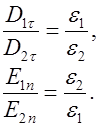 (3.20)
(3.20)
На границе раздела диэлектриков линии смещения преломляются (см. рис. 3.6).
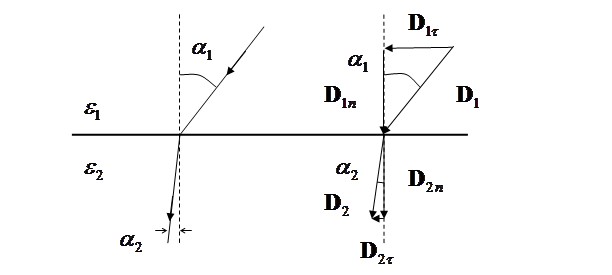
Рис. 3.6. Преломление линий электрического смещения на
границе раздела диэлектриков (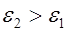 )
)
Формулы закона преломления линий смещения следуют из (3.18) – (3.20):
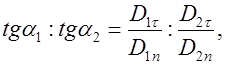
откуда
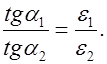 (3.21)
(3.21)
Для ослабления влияния внешнего электрического поля на электрический прибор можно поместить этот прибор внутрь оболочки из диэлектрика с большим значением 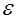 (см. рис. 3.7).
(см. рис. 3.7).
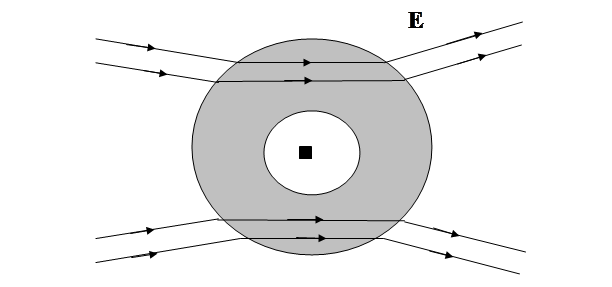
Рис. 3.7. Напряженность поля в воздушной полости внутри диэлектрика с 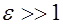 намного меньше, чем в воздухе, но вне диэлектрика
намного меньше, чем в воздухе, но вне диэлектрика
 2014-02-10
2014-02-10 6610
6610








