Автогенераторы с распределенной колебательной системой

Практически важной разновидностью автогенераторов с внутренней обратной связью служат автоколебательные устройства с применением отрезка линии передачи с распределенными параметрами. Типичный пример – лазер – автогенератор гармонических колебаний в оптическом и инфракрасном диапазонах. Лазер образован распределенной колебательной системой - резонатором (интерферометром) Фабри-Перо, между двумя полупрозрачными зеркалами. Пространство между зеркалами заполнено активной средой. Так в гелий-неоновом лазере используется смесь газов 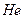и 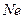. Накачкой энергии, например, - облучением, в среде может быть создана инверсная населенность энергетических уровней атомов или молекул. Устройство лазера показано на рис. 5.22

После создания инверсной населенности энергетических уровней атомы совершают вынужденные переходы с возбужденных уровней в более низкое энергетическое состояние под действием электромагнитного поля в резонаторе. Это поле – результат наложения полей, излучаемых большим числом атомов активной среды, друг на друга. Вынужденный, а не спонтанный характер излучения обеспечивает высокую степень пространственно-временной когерентности излучения лазера. Условие самовозбуждения лазера – мощность, излучаемая активной средой в резонатор, должна быть больше полной мощности потерь в системе.

Рис. 5.22

1 – полупрозрачное зеркало, 2 – активная среда, 3 – генерируемый пучок света

Рассмотрим гармонические волны в активной линии передачи. Амплитуда волны изменяется по закону 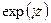в направлении оси 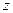, где 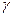- комплексная постоянная распространения, 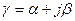. Колебания в каждой точке происходят по гармоническому закону 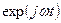. На эквивалентной схеме активную линию передачи можно представить отрезком длинной линии с погонными активным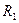и (и 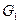) и реактивным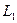и (и 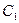) параметрами. По линии распространяются волны тока и напряжения. Из теории длинных линий известно, что 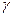зависит от погонных параметров линии как:

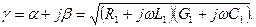(5.41)

Активность среды, выражающуюся в инверсной населенности энергетических уровней атомов, в данной модели можно учесть, полагая погонную шунтирующую проводимость 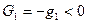. Выражение (5.41) можно переписать как

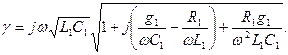(5.42)

Пусть линия передачи слабо отличается от идеальной, то есть 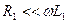и 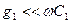. Тогда в (5.42) можно пренебречь третьим слагаемым под знаком радикала по сравнению с первыми двумя и получить приближенно:

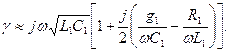(5.43)

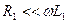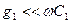При сделанных предположениях: и , параметры 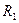и 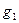пренебрежимо мало изменяют фазовую скорость волны в линии: 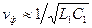, и коэффициент фазы: 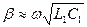. Так как 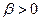, то изучаемая волна распространяется против оси 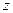. Однако значение , как видно из (5.43), существенно зависит от значения :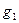

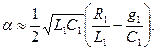(5.44)

Самовозбуждение означает, что за счет взаимодействия с активной средой амплитуда волны должна возрастать по направлению распространения волны. Значит, для волны, распространяющейся против оси 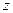, самовозбуждение наступает при 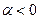, то есть при

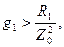(5.45)

где - волновое сопротивление линии, .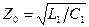

Из последней формулы следует, что чем меньше , тем большее значения модуля 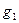отрицательной активной проводимости 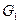необходимо для самовозбуждения распределенного автогенератора.