
10101101.1012 = 1 27+ 0
27+ 0 26+ 1
26+ 1 25+ 0
25+ 0 24+ 1
24+ 1 23+ 1
23+ 1 22+ 0
22+ 0 21+ 1
21+ 1 20+ 1
20+ 1 2-1+ 0
2-1+ 0 2-2+ 1
2-2+ 1 2-3 = 173.62510
2-3 = 173.62510
б) Перевести 703.048 "10" с.с.
"10" с.с.
703.048 = 7 82+ 0
82+ 0 81+ 3
81+ 3 80+ 0
80+ 0 8-1+ 4
8-1+ 4 8-2 = 451.062510
8-2 = 451.062510
в) Перевести B2E.416 "10" с.с.
"10" с.с.
B2E.416 = 11 162+ 2
162+ 2 161+ 14
161+ 14 160+ 4
160+ 4 16-1 = 2862.2510
16-1 = 2862.2510
Перевод целых десятичных чисел в недесятичную систему счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.
Примеры.
а) Перевести 18110 "8" с.с.
"8" с.с.
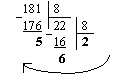 Результат: 18110 = 2658
Результат: 18110 = 2658
б) Перевести 62210 "16" с.с.
"16" с.с.
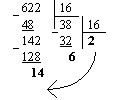 Результат: 62210 = 26E16
Результат: 62210 = 26E16
Перевод правильных дробей из десятичной системы счисления в недесятичную. Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.
Пример.
Перевести 0.312510 "8" с.с.
"8" с.с.
|
|
|
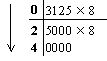
Результат: 0.312510 = 0.248
Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.
Пример.
Перевести 0.6510 "2" с.с. Точность 6 знаков.
"2" с.с. Точность 6 знаков.
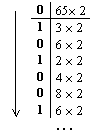 Результат: 0.6510
Результат: 0.6510 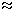 0.10(1001)2
0.10(1001)2
Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.
Пример.
Перевести 23.12510 "2" с.с.
"2" с.с.
| 1) Переведем целую часть: | 2) Переведем дробную часть: |
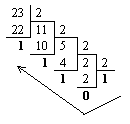
| 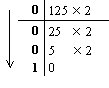
|
Итак: 2310 = 101112; 0.12510 = 0.0012. Результат: 23.12510 = 10111.0012.
Замечание. Необходимо отметить, что целые числа остаются целыми, а правильные дроби - дробями в любой системе счисления.
Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (Таблица 1) или четырехразрядным двоичным числом (тетрадой) (Таблица 1), при этом отбрасывают ненужные нули в старших и младших разрядах.
Примеры.
а) Перевести 305.48 "2" с.с.
"2" с.с.
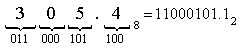
б) Перевести 7B2.E16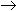 "2" с.с.
"2" с.с.
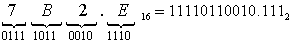
Для перехода от двоичной к восьмеричной (шестнадцатеричной) системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя (при необходимости) нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатерич–ной) цифрой.
Примеры.
а) Перевести 1101111001.11012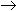 "8" с.с.
"8" с.с.
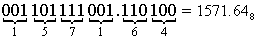
б) Перевести 11111111011.1001112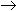 "16" с.с.
"16" с.с.
|
|
|
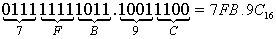
Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад.
Пример.
Перевести 175.248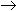 "16" с.с.
"16" с.с.
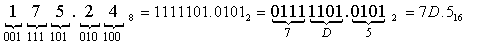
Результат: 175.248 = 7D.516.
 2014-02-10
2014-02-10 380
380








