Непрерывного линейного дрейфа

Планирование эксперимента в условиях

10. Планирование. При непрерывном временном дрейфе влияние управляемых переменных на выходную функцию у заметно сказывается уже при переходе от опыта к опыту. Простейшим случаем непрерывного дрейфа является линейный дрейф.

Рис. 5.1

Планирование эксперимента ортогонально линейному дрейфу проводят с помощью матрицы планирования ПФЭ типа N=2^Lчто оказывается возможным, если при каждом последующем измерении составляющая линейного дрейфа изменяется на одну и ту же величину Dy_t. Выполнение этого условия не встречает особых затруднений и может быть достигнуто экспериментированием через строго определенные, равные промежутки времени Dt= const (рис. 5.1). Величину Dt выбирают из условия 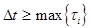, где 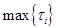—максимальное эквивалентное запаздывание реакции отклика по i-му каналу. Можно легко показать, что в этом случае линейный дрейф представим в виде ступенчатой функции (с N уровнями) и для представления этой функции необходимо L = log₂N первых столбцов (не считая нулевого) матрицы ПФЭ (см. табл.:5.2). Описание дрейфа имеет вид

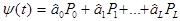, (5.8)

где 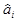(i=0, 1,..., L)—оценки коэффициентов, определяемые обычными методами. Оставшиеся столбцы матрицы можно использовать для планирования эксперимента. Правило получения планирования, ортогонального линейному дрейфу, заключается в следующем:

1) составляют матрицу ПФЭ типа N=2^L из условия 2^L³L+r, где r—число определяемых основных эффектов (линейных и взаимодействий);

2) первые L+1 столбцов используют для представления дрейфа;

3) оставшаяся часть матрицы есть искомое планирование, позволяющее определить коэффициенты неполной квадратичной модели.

Указанные положения для объекта с двумя факторами в случае N=2³=8 иллюстрирует табл. 5.2.

Таблица 5.2

Номер строки g Время t		Дрейф	Планирование
		Po	P1	P2	P3	z1	z2	z1z2
		u0	u1	u2	u3	u1u2	u1u3	u2u3	u1u2u3
t1 t2 t3 t4 t5 t6 t7 t8		+1 +1 +1 +1 +1 +1 +1 +1	-1 +1 -1 +1 -1 +1 -1 +1	-1 -1 +1 +1 -1 -1 +1 +1	-1 -1 -1 -1 +1 +1 +1 +1	+1 -1 -1 +1 +1 -1 -1 +1	+1 -1 +1 -1 -1 +1 -1 +1	+1 +1 -1 -1 -1 -1 +1 +1	-1 +1 +1 -1 +1 -1 -1 +1

Предлагаемый план дает возможность получит уравнение «истинной зависимости».

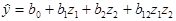, (5.9)

коэффициенты которой определяются независимо от дрейфа (а _о=b_o).

Общее уравнение связи для такого «дрейфующего» объекта имеет вид

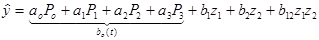(5.10)

где b_o(t) — изменение свободного члена b_o — определяет смещение поверхности отклика во времени.

2°. Проведение эксперимента. Опыты при линейном дрейфе надо выполнять строго последовательно во времени через равные интервалы Dt согласно составленному плану типа табл. 5.2.

Примечание. В моделирующем устройстве СМОУ-ГМЭИ генератор линейного дрейфа делает один шаг при нажатии кнопки «Пуск». Таким образом, каждому эксперименту соответствует определенное значение дрейфа. Из вышеизложенного следует, что при выполнении работы строки матрицы планирования реализуются строго последовательно, что соответствует требованию проведения экспериментов через равные промежутки времени, так как каждое нажатие кнопки «Пуск» соответствует интервалу времени Dt.

3°. Проверка воспроизводимости. Поскольку при экспериментировании в условиях непрерывного дрейфа дублирование экспериментов невозможно, проверку воспроизводимости не производят.

4°. Получение математической модели. Расчет оценок коэффициентов модели производят по известным формулам типа

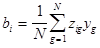. (5.11)

Значимость всех коэффициентов проверяют с помощью t-критерия Стьюдента:

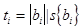. (5.12)

Дисперсию определения коэффициентов 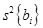находят по формуле

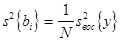. (5.13)

Значение дисперсии воспроизводимости опыта 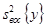берут из какого-либо другого опыта со своим числом степеней свободы. Так, например,.можно использовать дисперсию 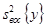определенную при экспериментировании в условиях блокового дрейфа с числом степеней свободы n_вос=n_зн=N_бл(m-1).

Вычисляя коэффициенты а_i по формуле (5.11), можно проверить гипотезу линейности дрейфа, высказанную априори. Эта гипотеза верна, если равенство

a _i+1=0,5 a _i (5.14)

удовлетворяется достаточно хорошо.

5°. Проверка адекватности. В том случае, если число членов аппроксимирующего уравнения (5.10) меньше числа опытов N, адекватность математического описания «дрейфующего» объекта проверяют с помощью F-критерия Фишера (см. тему 3). Дисперсию опыта 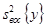берут из какого-либо другого опыта, проведенного на этом объекте, со своим числом степеней свободы. Так как при экспериментировании в условиях линейного дрейфа параллельные опыты не производятся, то в этом случае дисперсии определения коэффициентов велики, что может повлечь за собой увеличение числа незначимых коэффициентов. Проверку адекватности уравнения производят с исключенными из него незначимыми коэффициентами. Если это математическое описание оказывается не адекватным опытным данным, то следует произвести проверку адекватности уравнения с включенными в него незначимыми коэффициентами.