Контрольные вопросы и задачи
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Что такое активная мощность?
- Что такое реактивная мощность, с какими элементами она связана?
- Что такое полная мощность?
- Почему необходимо стремиться к повышению коэффициента мощности
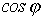 ?
? - Критерием чего служит баланс мощностей?
- К источнику с напряжением
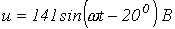 подключена активно-индуктивная нагрузка, ток в которой
подключена активно-индуктивная нагрузка, ток в которой 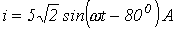 . Определить активную, реактивную и полную мощности.
. Определить активную, реактивную и полную мощности.
Ответ: Р=250 Вт; Q=433 ВАр; S=500 ВА.
- В ветви, содержащей последовательно соединенные резистор R и катушку индуктивности L, ток I=2 A. Напряжение на зажимах ветви U=100 B, а потребляемая мощность Р=120 Вт. Определить сопротивления R и XL элементов ветви.
Ответ: R=30 Ом; XL=40 Ом.
- Мощность, потребляемая цепью, состоящей из параллельно соединенных конденсатора и резистора, Р=90 Вт. Ток в неразветвленной части цепи I1=5 A, а в ветви с резистором I2=4 A. Определить сопротивления R и XL элементов цепи.
Ответ: R=10 Ом; XС=7,5 Ом.
| Лекция N 8. Резонансы в цепях синусоидального тока. |
Резонансом называется такой режим работы цепи, включающей в себя индуктивные и емкостные элементы, при котором ее входное сопротивление (входная проводимость) вещественно. Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением.
Резонанс в цепи с последовательно соединенными элементами (резонанс напряжений)
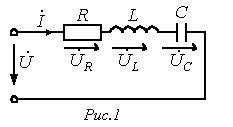 Для цепи на рис.1 имеет место Для цепи на рис.1 имеет место
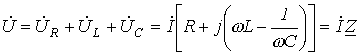 где
где
В зависимости от соотношения величин 1. В цепи преобладает индуктивность, т.е.
2. В цепи преобладает емкость, т.е. 3. Условие резонанса напряжений
При этом, как следует из (1) и (2), При резонансе напряжений или режимах, близких к нему, ток в цепи резко возрастает. В теоретическом случае при R=0 его величина стремится к бесконечности. Соответственно возрастанию тока увеличиваются напряжения на индуктивном и емкостном элементах, которые могут во много раз превысить величину напряжения источника питания. Пусть, например, в цепи на рис. 1 Явление резонанса находит полезное применение на практике, в частности в радиотехнике. Однако, если он возникает стихийно, то может привести к аварийным режимам вследствие появления больших перенапряжений и сверхтоков. Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной. Суть дела не меняется, если в цепи имеется несколько индуктивных и емкостных элементов. Действительно, в этом случае Как показывает анализ уравнения (3), режима резонанса можно добиться путем изменения параметров L и C, а также частоты. На основании (3) для резонансной частоты можно записать
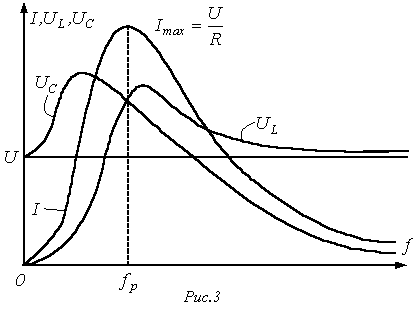
Резонансными кривыми называются зависимости тока и напряжения от частоты. В качестве их примера на рис. 3 приведены типовые кривые I(f); Важной характеристикой резонансного контура является добротность Q, определяемая отношением напряжения на индуктивном (емкостном) элементе к входному напряжению:
- и характеризующая “избирательные” свойства резонансного контура, в частности его полосу пропускания Другим параметром резонансного контура является характеристическое сопротивление, связанное с добротностью соотношением
или с учетом (4) и (5) для
Резонанс в цепи с параллельно соединенными элементами
где
В зависимости от соотношения величин
В цепи преобладает индуктивность, т.е. В цепи преобладает емкость, т.е.
Условие резонанса токов
При этом, как следует из (8) и (9), Идентичность соотношений (3) и (5) указывает, что в обоих случаях резонансная частота определяется соотношением (4). Однако не следует использовать выражение (4) для любой резонансной цепи. Оно справедливо только для простейших схем с последовательным или параллельным соединением индуктивного и емкостного элементов. При определении резонансной частоты в цепи произвольной конфигурации или, в общем случае, соотношения параметров схемы в режиме резонанса следует исходить из условия вещественности входного сопротивления (входной проводимости) цепи.
Поскольку в режиме резонанса мнимая часть
откуда, в частности, находится резонансная частота. Условие резонанса для сложной цепи со смешанным соединением нескольких индуктивных и емкостных элементов, заключающееся в равенстве нулю мнимой части входного сопротивления При определении резонансных частот для реактивного двухполюсника аналитическое выражение его входного реактивного сопротивления В качестве примера определим резонансные частоты для цепи рис. 7. Выражение входного сопротивления данной цепи имеет вид
 Сейчас читают про:
|
 2014-02-10
2014-02-10 424
424
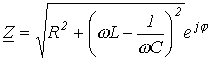 ;
;
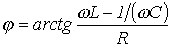 .
.
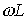 и
и 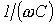 возможны три различных случая.
возможны три различных случая.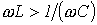 , а следовательно,
, а следовательно,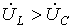 . Этому режиму соответствует векторная диаграмма на рис. 2,а.
. Этому режиму соответствует векторная диаграмма на рис. 2,а.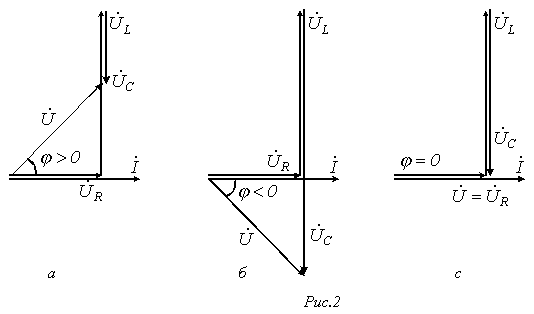
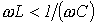 , а значит,
, а значит, 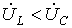 . Этот случай отражает векторная диаграмма на рис. 2,б.
. Этот случай отражает векторная диаграмма на рис. 2,б.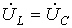 - случай резонанса напряжений (рис. 2,в).
- случай резонанса напряжений (рис. 2,в).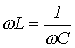 .
.
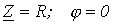 .
.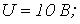
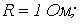
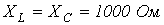 . Тогда
. Тогда 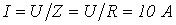 , и, соответственно,
, и, соответственно, 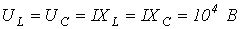 .
.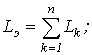
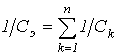 , и соотношение (3) выполняется для эквивалентных значений LЭ и CЭ .
, и соотношение (3) выполняется для эквивалентных значений LЭ и CЭ .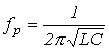 .
.
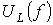 и
и 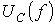 для цепи на рис. 1 при U=const.
для цепи на рис. 1 при U=const.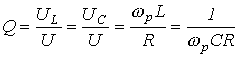 ,
,
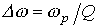 .
.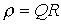 ,
,
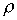 можно записать:
можно записать: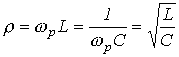 .
.
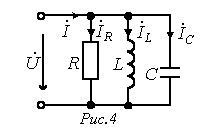 Для цепи рис. 4 имеем
Для цепи рис. 4 имеем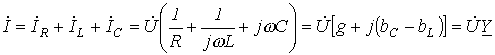 ,
,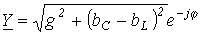 ;
;
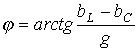 .
.
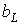 и
и  , как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.
, как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.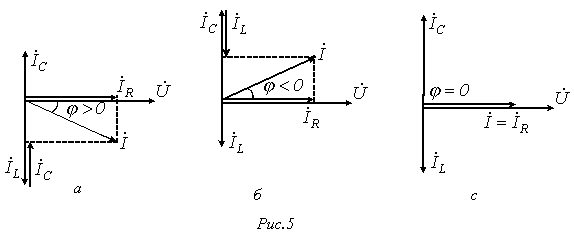
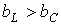 , а следовательно,
, а следовательно, 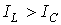 . Этому режиму соответствует векторная диаграмма на рис. 5,а.
. Этому режиму соответствует векторная диаграмма на рис. 5,а.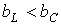 , а значит,
, а значит, 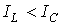 . Этот случай иллюстрирует векторная диаграмма на рис. 5,б.
. Этот случай иллюстрирует векторная диаграмма на рис. 5,б.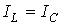 - случай резонанса токов (рис. 5,в).
- случай резонанса токов (рис. 5,в).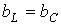 или
или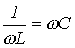 .
.
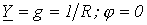 . Таким образом, при резонансе токов входная проводимость цепи минимальна, а входное сопротивление, наоборот, максимально. В частности при отсутствии в цепи на рис. 4 резистора R ее входное сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе токов ток на входе цепи минимален.
. Таким образом, при резонансе токов входная проводимость цепи минимальна, а входное сопротивление, наоборот, максимально. В частности при отсутствии в цепи на рис. 4 резистора R ее входное сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе токов ток на входе цепи минимален.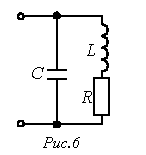 Например, для цепи на рис. 6 имеем
Например, для цепи на рис. 6 имеем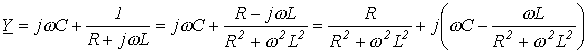
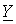 должна быть равна нулю, то условие резонанса имеет вид
должна быть равна нулю, то условие резонанса имеет вид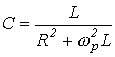 ,
,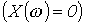 или входной проводимости
или входной проводимости 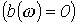 , определяет наличие у соответствующих этому условию уравнений относительно
, определяет наличие у соответствующих этому условию уравнений относительно 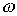 нескольких вещественных корней, т.е. таким цепям соответствует несколько резонансных частот.
нескольких вещественных корней, т.е. таким цепям соответствует несколько резонансных частот. или входной реактивной проводимости
или входной реактивной проводимости 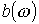 следует представить в виде отношения двух полиномов по степеням
следует представить в виде отношения двух полиномов по степеням 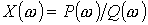 или
или 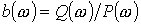 . Тогда корни уравнения
. Тогда корни уравнения 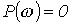 дадут значения частот, которые соответствуют резонансам напряжений, а корни уравнения
дадут значения частот, которые соответствуют резонансам напряжений, а корни уравнения 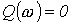 - значения частот, при которых возникают резонансы токов. Общее число резонансных частот в цепи на единицу меньше количества индуктивных и емкостных элементов в схеме, получаемой из исходной путем ее сведения к цепи (с помощью эквивалентных преобразований) с минимальным числом этих элементов. Характерным при этом является тот факт, что режимы резонансов напряжений и токов чередуются.
- значения частот, при которых возникают резонансы токов. Общее число резонансных частот в цепи на единицу меньше количества индуктивных и емкостных элементов в схеме, получаемой из исходной путем ее сведения к цепи (с помощью эквивалентных преобразований) с минимальным числом этих элементов. Характерным при этом является тот факт, что режимы резонансов напряжений и токов чередуются.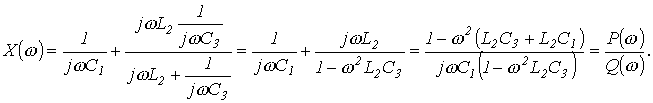
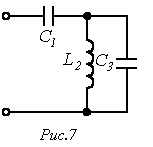 Из решения уравнения
Из решения уравнения 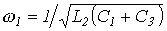 , соответствующую резонансу напряжений, а из решения уравнения
, соответствующую резонансу напряжений, а из решения уравнения 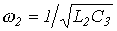 , соответствующую резонансу токов.
, соответствующую резонансу токов.





