Контрольные вопросы
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
- Какое поле называется пульсирующим?
- Какое поле называется вращающимся круговым?
- Какие условия необходимы для создания кругового вращающегося магнитного поля?
- Какой принцип действия у асинхронного двигателя с короткозамкнутым ротором?
- Какой принцип действия у синхронного двигателя?
- На какие синхронные скорости выпускаются в нашей стране двигатели переменного тока общепромышленного исполнения?
| Лекция N 22. Линейные электрические цепи при несинусоидальных периодических токах. |
Предыдущие лекции были посвящены анализу электрических цепей при синусоидальных токах и напряжениях. На практике ЭДС и токи в большей или меньшей степени являются несинусоидальными. Это связано с тем, что реальные генераторы не обеспечивают, строго говоря, синусоидальной формы кривых напряжения, а с другой стороны, наличие нелинейных элементов в цепи обусловливает искажение формы токов даже при синусоидальных ЭДС источников.
На практике к несинусоидальности напряжений и токов следует подходить двояко:
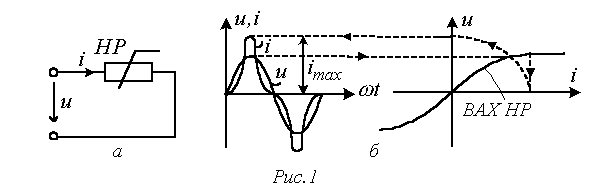 Характеристики несинусоидальных величин
Для характеристики несинусоидальных периодических переменных служат следующие величины и коэффициенты (приведены на примере периодического тока):
Характеристики несинусоидальных величин
Для характеристики несинусоидальных периодических переменных служат следующие величины и коэффициенты (приведены на примере периодического тока):
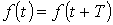 , где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверку на их выполнение проводить не нужно.
При разложении в ряд Фурье функция представляется следующим образом: , где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверку на их выполнение проводить не нужно.
При разложении в ряд Фурье функция представляется следующим образом:
Здесь В выражении (1)
Коэффициенты ряда Фурье для стандартных функций могут быть взяты из справочной литературы или в общем случае рассчитаны по приведенным выше формулам. Однако в случае кривых, обладающих симметрией, задача существенно упрощается, поскольку из их разложения выпадают целые спектры гармоник. Знание свойств таких кривых позволяет существенно сэкономить время и ресурсы при вычислениях.
К данному типу относятся кривые, удовлетворяющие равенству
К данному типу относятся кривые, для которых выполняется равенство
К этому типу относятся кривые, удовлетворяющие равенству
 Сейчас читают про:
|
 2014-02-10
2014-02-10 783
783
 .
.  .
.  .
. 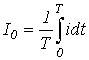 .
. 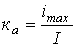 .
. 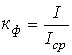 .
. 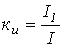 .
. 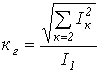 .
. 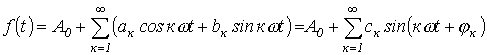 .
.
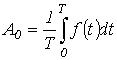 - постоянная составляющая или нулевая гармоника;
- постоянная составляющая или нулевая гармоника; 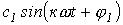 - первая (основная) гармоника, изменяющаяся с угловой частотой
- первая (основная) гармоника, изменяющаяся с угловой частотой  , где Т – период несинусоидальной периодической функции.
, где Т – период несинусоидальной периодической функции.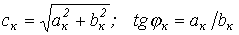 , где коэффициенты
, где коэффициенты 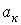 и
и 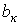 определяются по формулам
определяются по формулам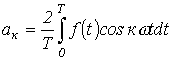 ;
; .
.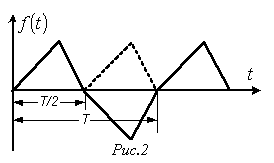 Кривые, симметричные относительно оси абсцисс.
Кривые, симметричные относительно оси абсцисс. 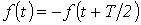 (см. пример на рис. 2). В их разложении отсутствуют постоянная составляющая и четные гармоники, т.е.
(см. пример на рис. 2). В их разложении отсутствуют постоянная составляющая и четные гармоники, т.е. 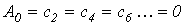 .
.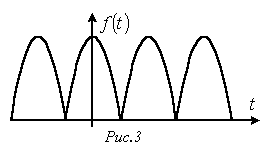 Кривые, симметричные относительно оси ординат.
Кривые, симметричные относительно оси ординат. 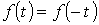 (см. пример на рис. 3). В их разложении отсутствуют синусные составляющие, т.е.
(см. пример на рис. 3). В их разложении отсутствуют синусные составляющие, т.е. 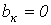 .
.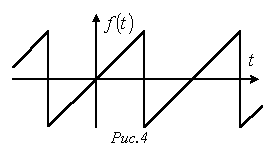 Кривые, симметричные относительно начала координат.
Кривые, симметричные относительно начала координат. 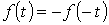 (см. пример на рис. 4). При разложении таких кривых отсутствуют постоянная и косинусные составляющие, т.е.
(см. пример на рис. 4). При разложении таких кривых отсутствуют постоянная и косинусные составляющие, т.е. 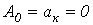 .
.





