2014-02-10
1599
Пусть нужно найти произведение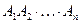 
последовательности 
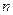матриц. Для перемножения двух матриц будем пользоваться стандартным алгоритмом, рассчитывая произведение «строки на столбец». Но прежде надо расставить скобки в произведении 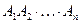, чтобы указать порядок умножений. Будем говорить, что в произведении матриц полностью расставлены скобки, если это произведение либо состоит из одной-единственной матрицы, либо является заключенным в скобки произведением двух произведений с полностью расставленными скобками. Поскольку умножение матриц ассоциативно, конечный результат вычислений не зависит от расстановки скобок. Например, в произведении 
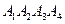можно полностью расставить скобки пятью разными способами:
,
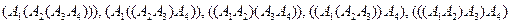во всех случаях ответ будет один и тот же.
Не влияя на ответ, способ расстановки скобок может сильно повлиять на стоимость перемножения матриц.
Если нужно перемножить матрицы размерносте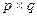й 
и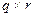 
, то стандартный алгоритм потребует 
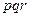умножений и примерно столько же сложений. Далее будем оценивать стоимость перемножения двух матриц числом умножений.
Чтобы увидеть, как расстановка скобок может влиять на стоимость, рассмотрим последовательность из трех матриц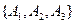 
размеров 10x100, 100х5 и 5х50 соответственно. При вычислении 
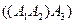нужно 
умножений, чтобы найти (10х5)-матрицу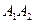 
, а затем 
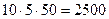умножений, чтобы умножить эту матрицу на 
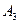. Всего 7500 умножений. При расстановке скобок 
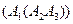мы делаем 
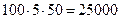умножений для нахождения (100х50)-матрицы 
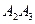, плюс ещё 
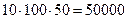умножений, итого 75000 умножений. Тем самым, первый способ расстановки скобок в 10 раз выгоднее.
Задача об умножении последовательности матриц может быть сформулирована следующим образом: дана последовательность из 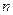матриц 
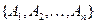заданных размеров (матрица 
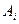имеет размер 
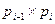); требуется найти такую (полную) расстановку скобок в произведении 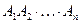, чтобы вычисление произведения требовало наименьшего числа умножений.
