Правильность алгоритма

Задача о выборе заявок

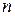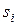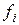Пусть даны заявок на проведение занятий в одной и той же аудитории. Два разных занятия не могут перекрываться по времени. В каждой заявке указаны начало и конец занятия (и для 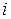-ой заявки). Разные заявки могут пересекаться, и тогда можно удовлетворить только одну из них. Мы отождествляем каждую заявку с промежутком 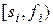, так что конец одного занятия может совпадать с началом другого, и это не считается пересечением.

Формально говоря, заявки с номерами 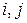совместны, если интервалы 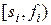и 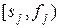не пересекаются (иными словами, ес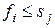ли / или 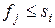). Задача о выборе заявок состоит в том, чтобы набрать максимальное количество совместных друг с другом заявок.

Жадный алгоритм работает следующим образом. Мы предполагаем, что заявки упорядочены в порядке возрастания времени окончания: 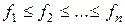. Если это не так, то можно отсортировать их за время 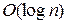. Заявки с одинаковым временем конца располагаем в произвольном порядке.

Тогда алгоритм выглядит так:

1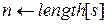

2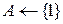

3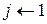

4 for 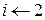to n

5 do if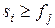

6 then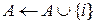

7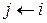

Множество 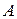состоит из номеров выбранных заявок, 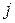— номер последней из них; при этом 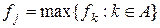, поскольку заявки отсортированы по возрастанию времени окончания. Вначале 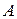содержит заявку номер 1, и 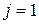(строки 2-3). Далее (строки 4-7) ищется заявка, начинающаяся не раньше окончания заявки номер 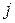. Если таковая найдена, она включается в множество 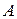и переменной 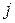присваивается её номер (строки 6-7).

Алгоритм требует всего лишь 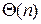шагов (не считая предварительной сортировки). Как и подобает жадному алгоритму, на каждом шаге он делает выбор так, чтобы остающееся свободным время было максимально.

Не для всех задач жадный алгоритм даёт оптимальное решение, но для нашей даёт. Убедимся в этом.

Напомним, что заявки отсортированы по возрастанию времени окончания. Прежде всего докажем, что существует оптимальное решение задачи о выборе заявок, содержащее заявку номер 1 (с самым ранним временем окончания). В самом деле, если в каком-то оптимальном множестве заявок заявка номер 1 не содержится, то можно заменить в нём заявку с самым ранним временем окончания на заявку номер 1. Это не повредит совместности заявок (ибо заявка номер 1 кончается ещё раньше, чем прежняя, и ни с чем пересечься не может) и не изменит их общего количества. Стало быть, можно искать оптимальное множество заявок 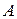среди содержащих заявку номер 1: существует оптимальное решение, начинающееся с жадного выбора.

После того как мы договорились рассматривать только наборы, содержащие заявку номер 1, все несовместные с ней заявки можно выкинуть, и задача сводится к выбору оптимального набора заявок из множества оставшихся заявок (совместных с заявкой номер 1). Другими словами, мы свели задачу к аналогичной задаче с меньшим числом заявок. Рассуждая по индукции, получаем, что, делая на каждом шаге жадный выбор, мы придём к оптимальному решению.