Пусть 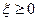 . Определим меру
. Определим меру 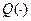 на
на 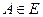 следующим образом:
следующим образом:
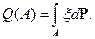
Если 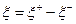 , то
, то 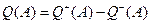 .
.
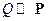 , следовательно, существует
, следовательно, существует
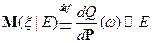
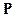 -п.н. единственна так называемая производная Радона-Никодима.
-п.н. единственна так называемая производная Радона-Никодима.
Заметим, что в том случае, если 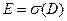 ,
,
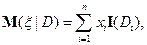
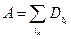 , то из пункта 2) определения
, то из пункта 2) определения
следует, что
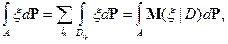
в том числе при 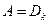
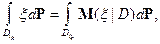
значит
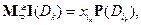
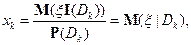
что и обобщает простой случай.
Все свойства условных математических ожиданий в общем случае совпадают со свойствами условных математических ожиданий для простых случайных величин.
Теорема о нормальной корреляции.
Для гауссовского вектора 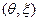 оптимальная оценка
оптимальная оценка 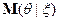 вектора
вектора 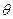 по
по  и её матрица ошибок
и её матрица ошибок
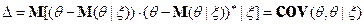
удовлетворяют следующим соотношениям:
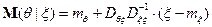
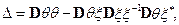
где 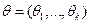 ,
, 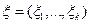 ,
, 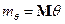 ;
; 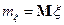 ;
; 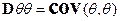 ;
; 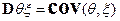 ;
; 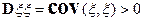 .
.
Доказательство. Образуем гауссовский вектор
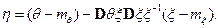
Из того, что 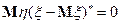 следует, что
следует, что 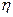 не коррелирует с
не коррелирует с 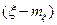 .
.
Так как 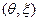 – гауссовский, то и
– гауссовский, то и 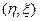 гауссовский, следовательно,
гауссовский, следовательно, 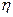 не зависит от
не зависит от 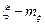 , значит
, значит 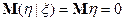 ;
;
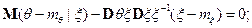
поэтому 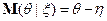 ;
; 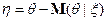 .
.
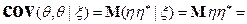
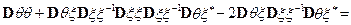
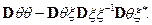
Теорема доказана.
Следствие. Для гауссовского вектора 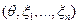 , где
, где 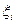 независимы,
независимы,
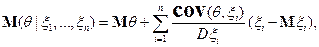
 2014-02-12
2014-02-12 265
265







