2014-02-12
828
Схема Калмана (частный случай).
На полном вероятностном пространстве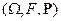 
пусть задан неубывающий поток 
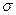-алгебр 
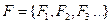, т.е.
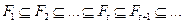и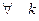 
, 
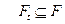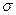– - алгебра.
Определение. Последовательность случайных величин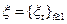 
называется 
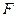-согласованным случайным процессом, если 
– - измеримая случайная величина.
Для упрощения можно предположить, что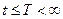 
. Пусть 
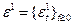и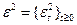 
– совместно-гауссовские независимые (и с независимыми по совокупности компонентами) стандартные случайные величины. Пусть при каждом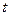 
порождается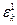 
и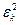 
, 
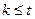, т.е. 
.
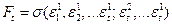Рассмотрим случайные (очевидно,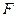-согласованные) процессы 
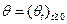и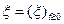 
,
определяемые рекурентной формулой: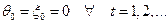 
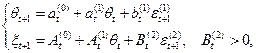
где 
- доступная наблюдению компонента, а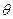 
- ненаблюдаема. Задача состоит в построении оценки
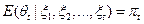
Обозначим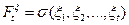 
. Тогда найдем
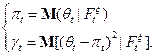
Теорема.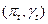 
удовлетворяет следующим уравнениям
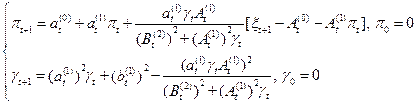
Доказательство. По теореме о нормальной корреляции
Но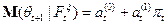 
, 
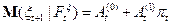по формулам схемы и из независимости 
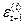от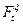 
. Найдем выражение для ковариаций.
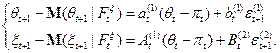
Следовательно
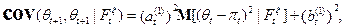
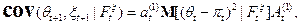
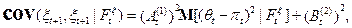
что и доказывает теорему.
Замечание. Теорема о нормальной корреляции в такой форме может рассматриваться не только как рекуррентная запись полной векторной теоремы о нормальной корреляции, но и как обобщенная теорема о нормальной корреляции, где линейные операторы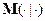 
заменяются на линейные операторы (с такими же для гауссовских векторов свойствами) 
с соответсвующей заменой 
на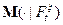 
.
Некоторые понятия теории случайных процессов.
1. 
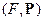- мартингалом называется случайный процесс 
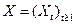, такой что
1) 
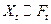
2) 
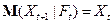
2. Процесс 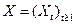называется марковским, если
1) 
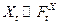с некоторой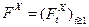 
2) 
.
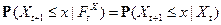3. Процедура (на полуинтуитивном уровне) построения винеровского процесса и пуассоновского процесса.
Винеровский процесс:
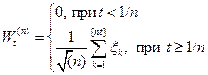
где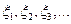 
- независимые одинаково распределенные случайные величины.
Литература
1. Колмогоров А.Н. Основные понятия теории вероятностей.-М.: Наука, 1974.
2. Ширяев А.Н. Вероятность.-М.: Наука, 1989.(1980 - 1-е изд.)
3. Боровков А.А. Теория вероятностей.-М.: Наука, 1986.
4. Гнеденко Б.В. Курс теории вероятностей.-М.: Наука, 1988.
5. Зубков А.М., Севастьянов Б.А., Чистяков В.П. Сборник задач по теории вероятностей.-М.: Наука, 1989.
