2014-02-09
509
III. Определение необходимой численности
Ошибка выборки зависит прежде всего от численности выборочной совокупности (n). Из формулы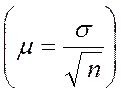 
видно, что средняя ошибка выборки обратно пропорциональна 
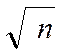. Поэтому при увеличении, например, численности выборки в четыре раза ее ошибка уменьшается вдвое.
Например: если бы мы отобрали из генеральной совокупности не 5%, а 2% единиц продукции, то численность выборки (n) оказалась бы равной 400 единицам. При условии, что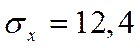 
размер ошибки для выборочной средней составит:
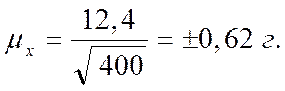
При отборе 5% изделий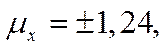 
а при отборе 20% изделий 
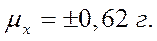, т.е. ошибка выборки уменьшилась в 2 раза. Увеличивая численность выборки, можно довести ее ошибку до сколь угодно малых размеров. Но с другой стороны, если в выборку войдет недостаточное количество образцов, то результаты исследования могут исказить характеристики генеральной совокупности.
Формулы расчета необходимой численности выборки определяются из предельной ошибки выборки. Так, применительно к формуле предельной ошибки средней при повторном отборе:
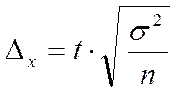
численность выборки получают путем решения этого равенства относительно n. Откуда необходимая численность выборки (n) составит:
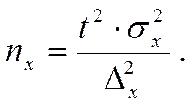
Применительно к формуле предельной ошибки доли для повторного отбора:
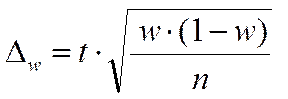
формула объема выборки для доли (n) имеет следующий вид:
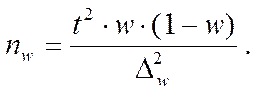
Численность выборки при бесповторном отборе.
Преобразования сводятся к определению значения n из формул предельной ошибки выборки:
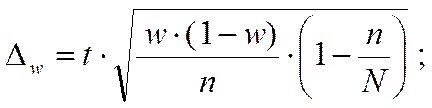
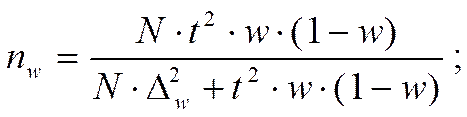
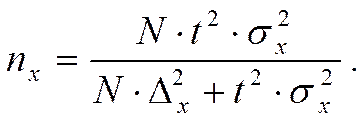
IV. Способы формирования выборочных
