Распределения Ферми–Дирака и Бозе–Эйнштейна.
В 1901 г. Дж. Гиббсом (J.W.Gibbs) в рамках классической статистики было открыто каноническое распределение частиц по энергиям:
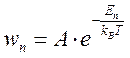 , (7.4)
, (7.4)
где En – энергия частицы макроскопической системы. Исходя из этого распределения, можно найти распределение по энергиям и в газе квантовых частиц – фермионов и бозонов.
Пусть в k -ом квантовом состоянии находятся nk частиц. Тогда, как известно из статистической физики, для этого состояния термодинамический потенциал W= F – m N (F – свободная энергия, m – химический потенциал, N – полное число частиц в системе) имеет вид:
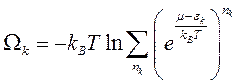 , (7.5)
, (7.5)
В идеальном газе фермионов действует принцип Паули, вследствие чего числа заполнения каждого состояния nk могут принимать лишь значения 0 или 1. Поэтому из (7.5) получаем
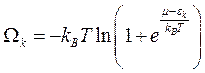
Производная термодинамического потенциала по химическому потенциалу определяет среднее число частиц, т.е.
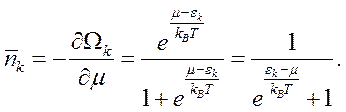 (7.6)
(7.6)
Выражение (7.6) описывает распределение частиц по уровням энергии в идеальном газе фермионов в зависимости от температуры и называется распределением Ферми–Дирака (рис. 7.1), которое в пренебрежении дискретностью состояний обычно записывается в виде:
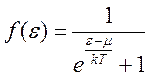 . (7.7)
. (7.7)
Распределение Ферми-Дирака нормировано очевидным условием
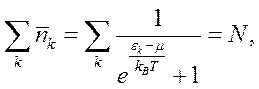
которое определяет в неявном виде химический потенциал m как функцию Т и N.
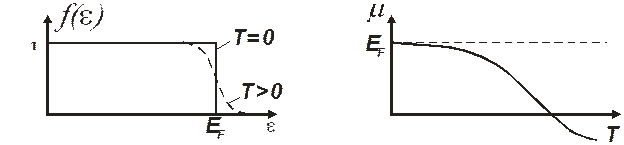 |
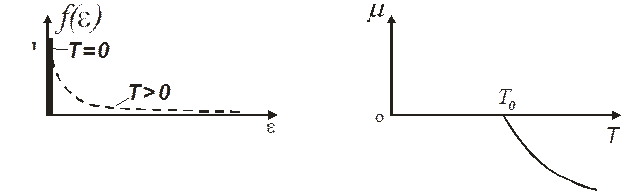
Из рис. 7.1 видно, что при Т =0К вероятность заселённости состояний f (ε) равна 1 и одинакова вплоть до энергии Ферми EF, а при отличных от нуля температурах вследствие тепловых возбуждений часть фермионов переходит в область энергий E>EF.

 Зависимость химического потенциала m, называемого также уровнем Ферми, от температуры показана на рис. 7.2.
Зависимость химического потенциала m, называемого также уровнем Ферми, от температуры показана на рис. 7.2.
Для частиц или комплексов частиц с целым спином (фотоны, фононы, 4Не2 и пр.) волновая функция симметрична относительно перестановок, и принцип Паули не действует. Числа заполнения квантовых состояний ничем не ограничены, поэтому (7.5) перепишем в виде
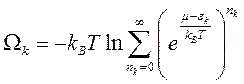 ,
,
где сумма геометрической прогрессии сходится только при
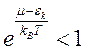 ,
,
что должно иметь место при любых e k, в том числе и при e k =0, следовательно, химический потенциал может быть только отрицательным, т.е. всегда m<0. Вычисляя сумму геометрической прогрессии, получим
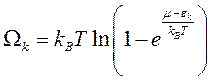 ,
,
откуда, аналогично (7.6) и (7.7), следует выражение для распределения по энергиям Бозе–Эйнштейна
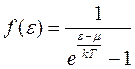 , (7.6)
, (7.6)
отличающееся от (7.5) знаком в знаменателе и другой зависимостью химического потенциала от температуры (рис. 7.3, 7.4).
У бозе-газа состояние с наименьшей энергией при Т =0К соответствует Е= 0 (так как m (T»0)=0), в отличие от ферми-газа, обладающего при Т»0 конечной энергией. Поэтому бозе-частицы при охлаждении с течением времени, отдавая энергию, собираются на нижнем энергетическом уровне (Е =0) с импульсом р= 0. Этот процесс называется «бозе-конденсацией», а получившееся в результате состояние системы частиц называется «бозе-конденсат».

 Главной особенностью бозе-конденсата является то, что все его частицы находятся на одном энергетическом уровне (при T =0), описываются одинаковой для всех частиц волновой функцией и, следовательно, сам бозе-конденсат описывается одной, общей для всех частиц, волновой функцией. При малых температурах (Т<T 0 =3.31 ћ2/mn2/3) распределение Бозе–Эйнштейна даёт экспоненциально спадающую (с ростом энергии) вероятность заселенности состояний:
Главной особенностью бозе-конденсата является то, что все его частицы находятся на одном энергетическом уровне (при T =0), описываются одинаковой для всех частиц волновой функцией и, следовательно, сам бозе-конденсат описывается одной, общей для всех частиц, волновой функцией. При малых температурах (Т<T 0 =3.31 ћ2/mn2/3) распределение Бозе–Эйнштейна даёт экспоненциально спадающую (с ростом энергии) вероятность заселенности состояний:
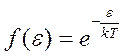 , (7.7 а)
, (7.7 а)
а при T>T 0вероятность заселенности состояний уменьшается гиперболически:
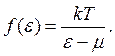 (7.7 б)
(7.7 б)
 2014-02-12
2014-02-12 1415
1415








