Изменение физических величин во времени

Лекция №7

Рассмотрим среднее значение физической величины L, изменяющееся во времени:

.

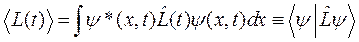Вычислим производную

.

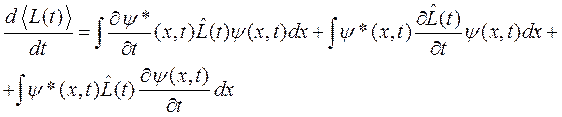Заменим в этом выражении производные волновых функций через гамильтониан из уравнения Шредингера:

.

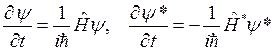Тогда

.

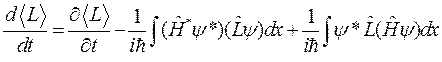Преобразуем первый интеграл, воспользовавшись самосопряженностью гамильтониана:

,

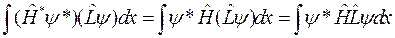что приводит к выражению

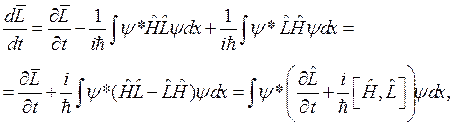
откуда получим выражение для производной оператора:

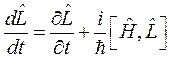
Определение

Если 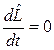, то соответствующая физическая величина L называется сохраняющейся или интегралом движения.

Следствия:

1.Если оператор 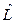явно не зависит от времени, то есть 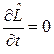, интегралом движения является величина, оператор которой коммутирует с , то есть

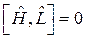
2. Положим 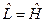, тогда, если гамильтониан не зависит от времени, то полная энергия системы сохраняется (замкнутая система).