Системы счисления. Рассмотрим более подробно формы представления чисел в повседневной жизни и в компьютере

Рассмотрим более подробно формы представления чисел в повседневной жизни и в компьютере.

Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.

Система счисления называется позиционной, если одна и та же цифра имеет различное значение, определяемое позицией цифры в последовательности цифр, изображающей число (примером непозиционной системы является римская система счисления).

Количество различных цифр в алфавите позиционной системы называется основанием S этой системы. Используемая в повседневной жизни система счисления имеет десять различных цифр (0,1,2,3,4,5,6,7,8,9) и поэтому называется десятичной системой счисления.

Любое число N в позиционной системе счисления может быть представлено суммой произведений целых однозначных коэффициентов a_i, взятых из алфавита системы на последовательные целые степени основания S:

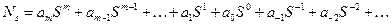(1.1.1)

Сокращенная запись числа N_s имеет вид:

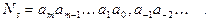
В этой последовательности запятая отделяет целую часть числа от дробной части. Запятая опускается, если нет отрицательных степеней. Позиции цифр a_i, отсчитываемые от запятой, называются разрядами. В позиционной системе счисления значение каждого разряда больше значения соседнего справа разряда в число раз, равное основанию S системы.

В компьютерах применяются следующие позиционные системы счисления: десятичная, двоичная, восьмеричная и шестнадцатеричная.

Алфавит десятичной системы счисления состоит, как уже указывалось, из десяти различных цифр: 0, 1, 2,... 9. В этой системе «вес» каждого разряда в 10 раз больше «веса» предыдущего. Например, в записи 1987 цифра 1 означает число тысяч, цифра 9 – число сотен, цифра 8 – число десятков и цифра 7 – число единиц.

Всякое число в десятичной системе счисления можно представить, в соответствие с формулой 1.1.1, суммой различных целых степеней десяти (S = 10) с соответствующими коэффициентами a_i (0, 1, 2,... 9):

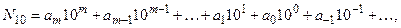
где

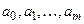– количество единиц, десятков, сотен и т. д.;

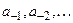– количество десятых, сотых, тысячных и т. д. долей единицы.

Иррациональные числа, например, число p, а также некоторые дроби, например, 1/3, не могут быть точно представлены с помощью конечной последовательности цифр. Как уже говорилось, в этом случае берется их приближение с заданной точностью.

Выбор той или иной системы счисления для представления чисел является произвольным. Так, выбор десятичной системы объясняется тем, что у нас на руках 10 пальцев. Однако разные народы в разные периоды времени использовали и другие системы счисления. Так, в древнем Вавилоне, наряду с десятичной системой счисления широко использовалась и шестидесятеричная система счисления. Следы шестидесятеричных дробей сохраняются и поныне в делении углового градуса, а также часа, на 60 минут и минуты на 60 секунд.

Ясно, что не существует максимального основания системы счисления, т.е. основание системы счисления может быть сколь угодно велико. В то же время существует минимальное основание системы счисления, равное 2. Эта система счисления называется двоичной системой счисления, в которой только две цифры – 0 и 1.

Любое действительное число в двоичной системе счисления представляется в виде суммы целых степеней основания S = 2, умноженных на соответствующие коэффициенты (0 или 1). Например, двоичное число 11011,01₂ представляется следующим образом:

11011,01₂ = 1×2⁴ + 1×2³ + 0×2² + 1×2¹ + 1×2⁰ + 0×2^-1 + 1×2^-2 =

= 16 + 8 + 2 + 1 + 0,25 = 27,25₁₀.

Для физического представления (изображения) чисел необходимы элементы, способные находиться в одном из нескольких устойчивых состояний. Число этих состояний должно быть равно основанию принятой системы счисления. Тогда каждое состояние будет представлять соответствующую цифру из алфавита данной системы счисления. Наиболее простыми с точки зрения технической реализации являются так называемые двухпозиционные элементы, способные находиться в одном из двух устойчивых состояний. Примерами таких двухпозиционных элементов могут служить:

· электромагнитное реле (состояния: замкнуто или разомкнуто);

· ферромагнитная поверхность (состояния: намагничена или размагничена);

· магнитный сердечник (состояния: намагничен в одном направлении или в противоположном);

· транзистор (состояния: проводит ток или не проводит тока).

Одно из этих устойчивых состояний может представлять цифру 0, а другое – цифру 1.

Именно простота и обеспечила наибольшее распространение в компьютерах двоичной системы счисления, основание которой S = 2; в ней используются лишь две цифры: 0 и 1.

Двоичное представление числа, по сравнению с десятичным представлением, требует большего числа разрядов (для многоразрядного числа примерно в 3,3 раза). Тем не менее, благодаря простоте, быстродействию и дешевизне технической реализации двухпозиционных элементов двоичная система счисления является в настоящее время основной системой, применяемой в компьютерах для представления информации, а также для выполнения арифметических и логических операций.

С помощью соответствующих программ десятичные числа при вводе в компьютер преобразуются в двоичные числа, а при выводе производится обратное преобразование. Однако при программировании и отладке программ часто приходится иметь дело с двоичными кодами команд программы, адресов и данных. Как уже говорилось, двоичные числа являются длинными и, кроме того, трудными для восприятия. Поэтому для сокращенной и удобной записи двоичных чисел часто используются восьмеричная и шестнадцатеричная системы счисления.

В восьмеричной системе счисления используются восемь цифр – от 0 до 7, а любое число представляется суммой целых степеней основания S = 8, умноженных на соответствующие коэффициенты a_i (0,1,...,7). Например, число 215₁₀ записывается в восьмеричной системе счисления следующим образом:

215₁₀ = 3×8² + 2×8¹ + 7×8⁰ = 327₈.

В шестнадцатеричной системе счисления алфавит цифровых знаков состоит из 16 символов, причем в качестве первых десяти символов используются арабские цифры от 0 до 9, а дополнительно к ним применяются буквенные символы: 10 – A(a), 11 – В(b), 12 – С(c), 13 – D(d), 14 – Е(e), 15 – F(f)

Число 215₁₀ в шестнадцатеричной системе счисления запишется следующим образом:

215₁₀ = D×16¹ + 7×16⁰ = D7₁₆.

Существуют различные способы перевода чисел из одной системы счисления в другую. Рассмотрим общие правила перевода из одной позиционной системы счисления в другую.

Перевод целого числа из десятичной системы счисления в систему с основанием Sосуществляется последовательным делением его на основание S новой системы счисления до тех пор, пока не получится частное, меньшее S. Число в новой системе запишется в виде остатков деления, начиная с последнего.

Перевод правильной дроби (меньшей 1) из десятичной системы счисления в систему с основанием Sосуществляется последовательным умножением ее на основание S, при этом перемножаются только дробные части. Дробь в новой системе счисления записывается в виде целых частей получающихся произведений, начиная с первого.

Для перевода неправильных дробей (больших 1) необходимо выполнить отдельно перевод целой и дробной частей.

При переводе деление и умножение выполняются в десятичной системе счисления.

Для перевода чисел из системы счисления S в десятичную систему счисления удобнее всего воспользоваться формулой 1.1.1.

Так как основания восьмеричной и шестнадцатеричной систем счисления соответствуют целым степеням числа 2 (8 = 2³; 16 = 2⁴), для них исключительно просты правила перевода в двоичную систему счисления, и наоборот. Каждые три цифры двоичного числа преобразуются в одну цифру восьмеричного числа справа налево (если длина двоичного числа не кратна трем, впереди добавляется соответствующее число нулей). При обратном преобразовании каждая цифра восьмеричного числа преобразуется в три двоичные цифры.

Аналогично выполняются взаимные преобразования шестнадцатеричных и двоичных чисел, за исключением того, что число двоичных цифр равно четырем.

Примеры перевода чисел из одной системы счисления в другую.

1. Перевод числа 377₁₀ в шестнадцатеричную систему счисления:

377:16 = 23 (остаток 9); 23:16 = 1 (остаток 7); 1:16 = 0 (остаток 1).

Результат: 179₁₆.

2. Перевод дроби 0,6875₁₀ в восьмеричную систему счисления:

0,6875×8 = 5,5000 (5); 0,5000×8 = 4,0000 (4).

Результат: 0,54₈.

3. Перевод числа FCA1₁₆ в десятичную систему счисления:

FCA1₁₆ = 15×16³ + 12×16² + 10×16¹ + 1×16⁰ =

= 61440 + 3072 + 160 + 1 = 64673₁₀.

4. Перевод числа 1111111₂ в шестнадцатеричную систему счисления:

1111111₂ = 0111 1111 = 7F₁₆.

5. Перевод числа 9C8₁₆ в двоичную систему счисления:

6C8₁₆ = 0110 1100 1000 = 11011001000₂.

Арифметические операции в системе счисления S выполняются так же, как и в десятичной системе, но необходимо учитывать, что при сложении и умножении единица переносится в старший разряд, когда сумма или произведение чисел больше основания S, а при вычитании в старшем разряде занимается количество единиц, также равное основанию S.

Примеры арифметических операций над шестнадцатеричными цифрами.

1. Сложение шестнадцатеричных чисел:

12A₁₆ + C48₁₆ = D72₁₆;

A₁₆ + 8₁₆ = 12₁₆; (перенос 1 в старший разряд);

2₁₆ + 4₁₆ + 1(из младшего разряда) = 7₁₆;

1₁₆ + C₁₆ = D₁₆;

2. Вычитание шестнадцатеричных чисел:

142₁₆ - С8₁₆ = 7A₁₆;

2₁₆ + 10₁₆ (заем из старшего разряда) - 8₁₆ = A₁₆;

4₁₆ - 1₁₆(занято в младший разряд) +

+ 10₁₆ (заем из старшего разряда) - С₁₆ = 7₁₆.