Метод наименьших квадратов. Обработка результатов эксперимента

Обработка результатов эксперимента

Тщательное, скрупулезное выполнение эксперимента, несомненно, является главным условием успеха исследо­вания. Это общее правило, и планирование эксперимента не относится к исключениям.

Однако нам не безразлично, как обработать полученные данные. Мы хотим навлечь из них всю информацию и сде­лать соответствующие выводы. Как всегда, мы находимся между Сциллой и Харибдой. С одной стороны, не извлечь из эксперимента все, что из него следует,– значит прене­бречь нелегким трудом экспериментатора. С другой стороны, сделать утверждения, не следующие из эксперимента, – значит создавать иллюзии, заниматься самообманом.

Статистические методы обработки результатов позво­ляют нам не перейти разумной меры риска.

Нач­нем с простого случая: один фактор, линейная модель. Интересующая нас функция отклика (которую мы будем также называть уравнением регрессии) имеет вид

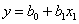
Это хорошо известное уравнение прямой линии. Наша цель – вычисление неизвестных коэффициентов b ₀и b ₁. Мы провели эксперимент, чтобы использовать при вычис­лениях его результаты. Как это сделать наилучшим обра­зом?

Если бы все экспериментальные точки лежали строго на прямой линии, то для каждой из них было бы справед­ливо равенство

,

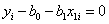где i = 1, 2,..., N – номер опыта. Тогда не было бы никакой проблемы. На практике это равенство нарушается и вместо него приходится писать

,

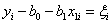где 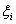– разность между экспериментальным и вычис­ленным по уравнению регрессии значениями y в i-й экспе­риментальной точке. Эту величину иногда невязкой.

Мы хотим найти такие коэффициенты регрессии, при которых невязки будут минимальны. Это требо­вание можно записать по-разному. В зависимости от этого мы будем получать разные оценки коэффициентов. Вот одна из возможных записей

,

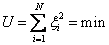которая приводит к методу наименьших квадратов.

Когда мы ставим эксперимент, то обычно стремимся провести больше (во всяком случае не меньше) опытов, чем число неизвестных коэффициентов. Поэтому система линейных уравнений

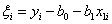
оказывается переопределенной и часто противоречивой (т. е. она может иметь бесконечно много решений или может не иметь решений). Переопределенность возникает, когда число уравнений больше числа неизвестных; противоре­чивость – когда некоторые из уравнений несовместимы друг с другом.

Только если все экспериментальные точки лежат па прямой, то система становится определенной и имеет единственное решение.

МНК обладает тем замечательным свойством, что он делает определенной любую, произвольную систему уравнений. Он делает число уравнений равным чис­лу неизвестных коэффициентов.

Для определения двух неизвестных коэф­фициентов требуется два уравнения. Давайте попробуем их получить.

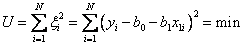
Мини­мум некоторой функции, если он существует, достигается при одновременном равенстве нулю частных производных по всей неизвестным, т. е.

.

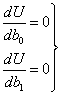В явном виде это запишется как

,

.

Окончательные формулы для вычисления коэффи­циентов регрессии, которые удобно находить с помощью определителей, имеют вид

,

.

Величина 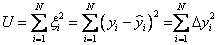называется остаточной суммой квадратов ( 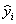– значение параметра оптимизации, вычисленное из уравнения регрессии). МНК гарантирует, что эта величина минимально возможная.

Обобщение на многофакторный случай не связано с какими-либо принципиальными трудностями.

Воспользуемся тем, что матрицы планирования ортогональны и нормированы, т.е.

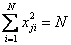и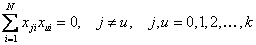

Для любого числа факторов коэффициенты будут вычисляться по формуле

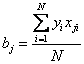
В этой формуле j = 0, 1, 2..., k – номер фактора. Ноль записан для вычисления b ₀.

Так как каждый фактор (кроме x ₀)варьируется на двух уровнях +1 и –1, то вычисления сводятся к приписыванию столбцу y знаков соответствующего фактору столбца и алгебраическому сложению полученных значений. Де­ление результата на число опытов в матрице планирова­ния дает искомый коэффициент.