Расчет среднего арифметического результатов тестирования

Таблица 3.3

№ пп	xi * (баллы)	ni	nixi *
			1 296
			2 280
			2 720
Сумма	7 712

Пример 3.9. Средний балл, полученный учащимися класса за кон­трольную работу, находится по формуле: B = 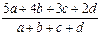, где a - число школь­ни­ков, получивших оценку "5"; b - число школьников, получивших оценку "4"; c -число школьников, получивших оценку "3"; d - число школьников, полу­чивших оценку "2".

Пример 3.10. На соревнованиях по фигурному катанию 2 фигуристки получили (по шестибалльной шкале) оценки судей, представленные в таблице на рис. 3.7. Которая из фигуристок выступила лучше?

Номер фигуристки	Номер судьи
	4,8	5,6	4,9	5,2	4,7	4,9	4,9	4,8	4,7
	5,1	4,2	5,0	4,9	5,0	5,1	5,0	5,1	5,0

Рис. 3.7

Решение. Запишем в таблицы (см. рис. 3.8) распределение по частотам оценок X и У, выставленных соответственно первой и второй фигури­сткам:

X	4,7	4,8	4,9	5,2	5,6		У	4,2	4,9	5,0	5,1
ni						ni

Рис. 3.8

Найдем среднее значение оценок каждой из фигуристок: ` x» 4,94;` y» 4,93. Видим, что` x > ` y. Хотя очевидно, что у второй фигуристки почти все оценки больше 5,0, а у первой – меньше 5,0. При этом сравнение в пользу второй фигуристки выглядит несправедливым. Такой результат получен, скорее всего, из-за необъективности 2-го судьи, завысившего по сравнению с остальными судьями оценку первой фигуристке и занизив­шего оценку второй фигуристке.

Для большей объективности сравнения результатов в по­следние годы на международных соревнованиях из совокуп­ности баллов каждого фигуриста отбрасывают наибольшее и наименьшее значения. После отбрасывания наибольшего и наименьшего значе­ний из совокупности баллов каждой фигуристки имеем: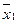» 4,89; » 5,01. Так как 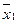< , считаем, что вторая фигуристка высту­пала лучше первой.

Ответ: вторая фигуристка высту­пала лучше первой.

■ Медиана (Me) определяется как показатель середины вариационного ряда. Напри­мер, при наличии в классе 25 учащихся это будет оценка результатов тринадцатого ученика в списке, где все ученики распределены по их ранговым оценкам. В ряду с четным числом членов медиана равна среднему арифмети­ческому двух центральных значений. Ясно, что медиана делит упорядоченный ряд чисел на две равные по количеству элементов части: в одной из них значения не больше медианы, в другой – не меньше медианы.

Медиана имеет свойство, значимое для решения при­кладных задач: сумма абсолютных величин отклонений от нее является для рассматри­ваемой совокупности мини­мальной.

■ Мода (Mо) – значение вариационного ряда, которое встречается наи­бо­лее часто. На­при­мер, для ряда на рис. 3.4 мода равна 7.

Если в выборке среднее значение существенно отличает­ся от моды, то его неразумно выбирать в качестве типично­го представителя сово­купности данных (чем больше значе­ние моды отличается от среднего, тем «более несимметри­чен» полигон частот совокупности).

■ Размах выборки (вариации) (w) – разность между мак­си­мальным и минимальным элемен­тами выборки, т.е. w = x_max – x_min. Инфор­мативность этого показателя невелика. Можно при­вести очень много распределений, сильно отличающихся по форме, но имеющих одинаковый размах.

Пример 3.11. Найдите размах, среднее, моду и медиану выборки, представленной в Примере 3.3.

Решение. Запишем предложенные значения в виде вариационного ряда: 2, 2, 2, 3, 4, 4, 5, 5, 5, 7, 7, 7, 7, 10, 10. Размах выборки w = 10 – 2 = 8; среднее` x = 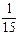· (3·2 + 1·3 + 2·4+ 3·5+ 4·7+ 2·10)» 5,3; наи­бо­лее часто встречается значение 7, значит, мода Мо = 7; середина вариационного ряда приходится на 8-й элемент, значит, медиана Me =5.

Ответ: w = 8;` x» 5,3; Мо = 7; Me =5.

■ Дисперсию (Dx) вычисляют по приведенным ниже формулам:

Для несгруппированных данных:

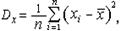для сгруппированных данных:

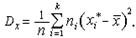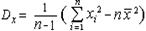На практике используют другие расчетные формулы. Для несгруппированных дан­ных:

(3.3)

или

(3.4)

Если данные сгруппированы

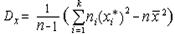(3.5)

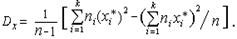или

(3.6)

Дисперсия равна среднему квадрату отклонений значения вари­анты от среднего значения. Она выступает как одна из характеристик ин­дивидуальных результатов разброса значений исследуемой пере­мен­ной (например, оценок учащихся) вокруг срднего значения. Зна­че­ние дисперсии используется в различных статистических расчетах, но не имеет непосредственно наблюдаемого характера. Величиной, непо­средственно связанной с содержанием наблюдаемой перемен­ной, является среднее квадратическое отклонение.

■ Стандартное отклонение (или среднеквадратическое отклонение) – положи­тель­ный квадратный корень из дисперсии: s =. Размерность стан­дартного откло­нения в отличие от размерности дисперсии совпа­дает с едини­цами измерения варьи­рующего признака, поэтому в практи­ческой статистике для ха­рактеристики рассеяния используют обычно стан­дартное отклонение, а не диспер­сию.

Пример 3.12. Найдите дисперсию и стандартное от­клонение результа­тов тестирования 15 учеников 3-го класса (см. Пример 3.7).

Решение. По формуле (3.4) получаем D_x = (772 987 – 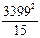)» 198,1 (балла²). Тогда s =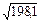» 14,1 (балла). Промежуточные расчеты приведены в таблице 3.4.

Ответ: D_x» 198,1 балла²; s»14,1 балла.