Отсечение нелицевых граней

Рассмотрим многогранник, для каждой грани которого задан вектор внешней нормали (рис. 12.5). Несложно заметить, что если вектор нормали грани 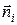(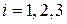) составляет с вектором 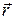, задающим направление проектирования, тупой угол, то эта грань заведомо не может быть видна. Такие грани называются не лицевыми. В случае, когда соответствующий угол является острым, грань называется лицевой.

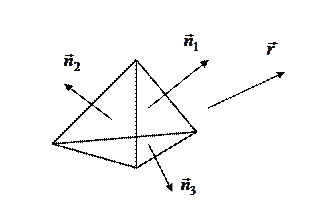Рис. 12.5	Рис. 12.6

Пусть 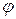– угол между вектором нормали 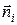к некоторой грани и направлением проектирования 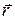, которые заданы в мировой системе координат.

Так как для случая параллельного проектирования направление проектирования не зависит от грани (значение вектора 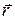не зависит от номера грани 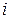), то условие отбора лицевой грани с номером 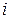можно записать в виде

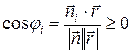, (12.1)

что говорит о том, что угол 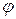является острым и его значение принадлежит отрезку 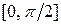. Поскольку знаменатель в (12.1) всегда положителен, то условие (12.1) можно заменить на более простое

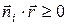(12.2)

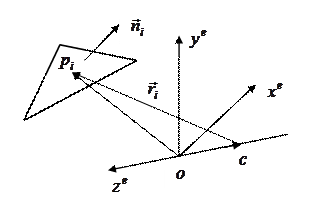
Рассмотрим случай центрального проектирования (рис. 12.6). Пусть для этого случая в видовой системе координат заданы: 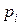– произвольная точка на некоторой грани с номером 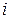, 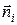– вектор внешней нормали к этой грани, 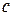– точка, определяющая центр проектирования, 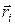– направление проектирования для точки 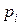, 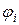– угол между вектором нормали 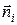и направлением проектирования 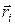. В отличие от случая параллельного проектирования значение вектора 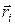зависит от положения точки 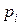на выбранной грани.

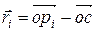(12.3)

Теперь можно записать условие отбора лицевой грани

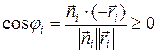(12.4)

или более просто

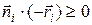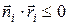() (12.5)

Знак этого скалярного произведения в (12.5) не зависит от выбора точки на грани, а определяется тем, в каком полупространстве относительно плоскости, содержащей данную грань, лежит центр проектирования. Поэтому, определения того, является заданная грань лицевой или нет, достаточно взять произвольную точку на этой грани и проверить выполнение условия (12.5)

В случае, когда фигура представляет собой один выпуклый многогранник, удаление не лицевых граней полностью решает задачу удаления невидимых граней.

В общем случае предложенный подход хотя и не решает задачу полностью, но позволяет примерно вдвое сократить количество рассматриваемых граней [].