Это означает рисование полигонов граней в порядке от самых дальних к самым близким. Этот метод не является универсальным, ибо иногда нельзя четко различить, какая грань ближе (рис. 12.7).
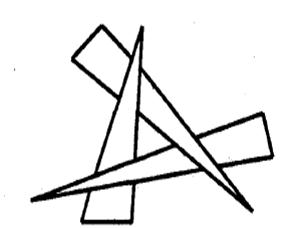 |  |
| Рис. 12.7 | Рис. 12.8 |
Известны модификации этого метода, которые позволяют корректно рисовать такие грани, они описаны в [28]. Метод сортировки по глубине эффективен для показа поверхностей (рис. 12.8), заданных функциями 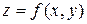 .
.
В качестве примера рассмотрим возможный вариант определения дальней грани в зависимости от положения наблюдателя для случая построения графика поверхности, определяемой функцией 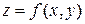 .
.
Пусть рассчитана матрица значений функции 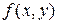 .
.
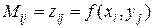 , (12.6)
, (12.6)
где
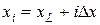 ,
, 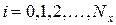 ,
, 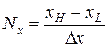 , (12.7)
, (12.7)
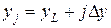 ,
, 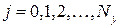 ,
, 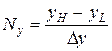 , (12.8)
, (12.8)
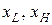 – соответственно нижняя и верхняя границы для изменения аргумента
– соответственно нижняя и верхняя границы для изменения аргумента 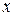 , а
, а 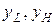 – нижняя и верхняя границы для изменения аргумента
– нижняя и верхняя границы для изменения аргумента 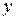 ,
, 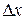 и
и 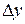 – интервалы дискретизации для аргументов
– интервалы дискретизации для аргументов 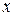 и
и 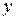 .
.
Далее, пусть 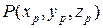 – точка в системе координат
– точка в системе координат 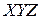 , где расположен наблюдатель, а
, где расположен наблюдатель, а 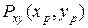 – проекция точки
– проекция точки 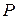 на плоскость
на плоскость 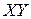 (рис. 1-2). На приведенных рисунках матрица
(рис. 1-2). На приведенных рисунках матрица 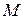 представлена прямоугольником
представлена прямоугольником 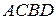 .
.
Через точки 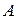 и
и 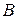 проведем прямую
проведем прямую 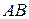 , уравнение которой будет иметь вид
, уравнение которой будет иметь вид
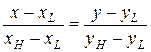
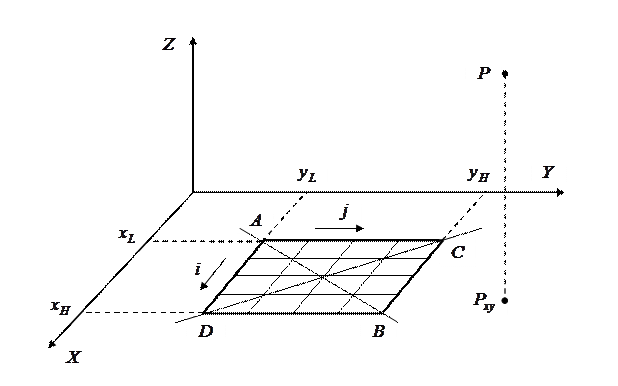
Рис. 12.9
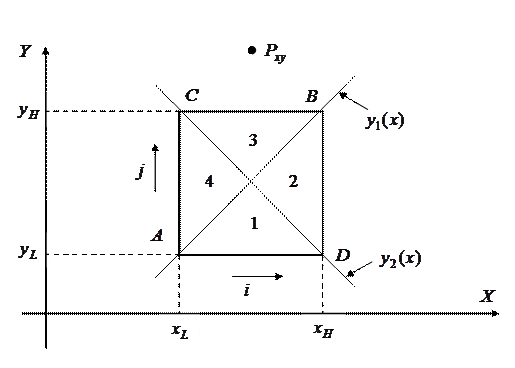
Рис. 12.10
или
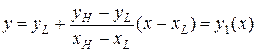 (12.9)
(12.9)
Аналогично через точки 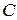 и
и 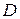 проведем прямую
проведем прямую 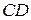 , уравнение которой будет иметь вид
, уравнение которой будет иметь вид
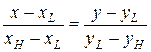
или
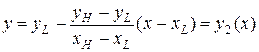 (12.10)
(12.10)
Прямые 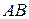 и
и 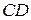 делят плоскость
делят плоскость 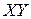 на четыре области: 1, 2, 3, 4 (рис. 12.10). Из рис. 12.10 видно, что дальняя грань определяется по отношению к расположению точки
на четыре области: 1, 2, 3, 4 (рис. 12.10). Из рис. 12.10 видно, что дальняя грань определяется по отношению к расположению точки 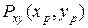 на плоскости
на плоскости 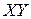 .
.
Если
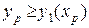 и
и 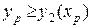 , то точка
, то точка 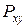 находится в области 3 и дальней является грань
находится в области 3 и дальней является грань 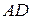 .
.
Если
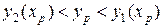 , то точка
, то точка 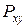 находится в области 2 и дальней является грань
находится в области 2 и дальней является грань 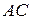 .
.
Если
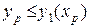 и
и 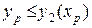 , то точка
, то точка 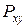 находится в области 1 и дальней является грань
находится в области 1 и дальней является грань 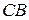 .
.
Если
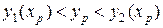 , то точка
, то точка 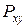 находится в области 4 и дальней является грань
находится в области 4 и дальней является грань 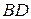 .
.
 2014-02-12
2014-02-12 1368
1368







