Прямая на плоскости и в пространстве является бесконечной в обе стороны. Лучом называется полупрямая, т.е. множество всех точек прямой, лежащих по одну сторону от заданной ее точки, называемой началом луча. Луч будем задавать в параметрическом виде, как это было описано в одном из предыдущих разделов. Пусть 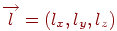 - направляющий вектор прямой, а
- направляющий вектор прямой, а 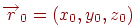 - начальная точка. Тогда координаты точек луча будут определяться формулами
- начальная точка. Тогда координаты точек луча будут определяться формулами
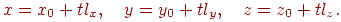 | (3.8) |
Будем считать, что направляющий вектор единичный, т.е.  .
.
Сначала рассмотрим задачу о нахождении точки пересечения луча с плоскостью, заданной каноническими уравнением
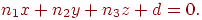 | (3.9) |
Вектор нормали 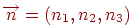 тоже будем считать единичным. Сначала надо определить значение параметра t, при котором луч пересекает плоскость. Для этого подставим координаты из формулы (3.8) в уравнение (3.9) и получим
тоже будем считать единичным. Сначала надо определить значение параметра t, при котором луч пересекает плоскость. Для этого подставим координаты из формулы (3.8) в уравнение (3.9) и получим
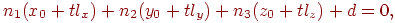
откуда легко определить, что луч пересекает плоскость в точке со значением
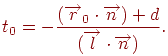
Очевидно, что такая точка существует только при условии 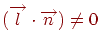 . В свою очередь, эта величина обращается в нуль только в случае, когда векторы
. В свою очередь, эта величина обращается в нуль только в случае, когда векторы 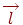 и
и 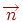 ортогональны друг другу.
ортогональны друг другу.
Пусть теперь нам задана сфера с центром в точке 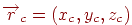 и радиусом
и радиусом 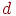 . Тогда уравнение сферы будет иметь вид
. Тогда уравнение сферы будет иметь вид
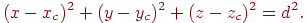
Подставив сюда координаты луча из уравнения (3.9), получим, что параметр, при котором луч пересекает сферу, должен удовлетворять квадратному уравнению
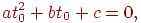
где 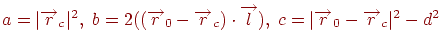 . Определим корни этого уравнения. Если дискриминант
. Определим корни этого уравнения. Если дискриминант 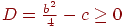 , то корни существуют. Их может быть либо два
, то корни существуют. Их может быть либо два 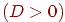 , либо один
, либо один 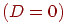 . В первом случае имеем две точки пересечения, во втором - одну (луч касается сферы). Соответствующие значения параметра определяются соотношением
. В первом случае имеем две точки пересечения, во втором - одну (луч касается сферы). Соответствующие значения параметра определяются соотношением
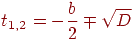
 2014-02-12
2014-02-12 5143
5143








