Множественная регрессия и корреляция. Таблица 1.5 Вид функции, Первая производная

Таблица 1.7

Таблица 1.6

Таблица 1.5

Таблица 1.5

Вид функции,	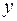Первая производная,	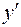Средний коэффициент эластичности,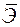

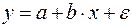
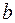
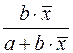
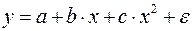
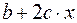
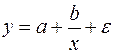
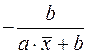
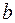
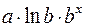
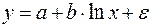
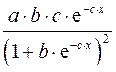
Возможны случаи, когда расчет коэффициента эластичности не имеет смысла. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения в процентах.

Уравнение нелинейной регрессии, так же, как и в случае линейной зависимости, дополняется показателем тесноты связи. В данном случае это индекс корреляции:

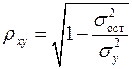, (1.21)

где 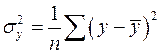– общая дисперсия результативного признака 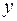, 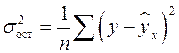– остаточная дисперсия.

Величина данного показателя находится в пределах: 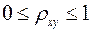. Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.

Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака 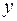, объясняемую регрессией, в общей дисперсии результативного признака:

, (1.22)

т.е. имеет тот же смысл, что и в линейной регрессии; .

Индекс детерминации можно сравнивать с коэффициентом детерминации для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина меньше . А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию.

Индекс детерминации используется для проверки существенности в целом уравнения регрессии по -критерию Фишера:

, (1.23)

где – индекс детерминации, – число наблюдений, – число параметров при переменной 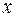. Фактическое значение -критерия (1.23) сравнивается с табличным при уровне значимости и числе степеней свободы (для остаточной суммы квадратов) и 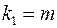(для факторной суммы квадратов).

О качестве нелинейного уравнения регрессии можно также судить и по средней ошибке аппроксимации, которая, так же как и в линейном случае, вычисляется по формуле (1.8).

Рассмотрим пример из параграфа 1.1, предположив, что связь между признаками носит нелинейный характер, и найдем параметры следующих нелинейных уравнени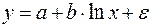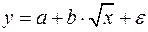й: , и .

Для нахождения параметров регрессии делаем замену и составляем вспомогательную таблицу ().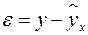

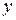
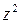
	1,2	0,182	0,9	0,164	0,033	0,81	0,499	0,401	0,1610	44,58
	3,1	1,131	1,2	1,358	1,280	1,44	1,508	-0,308	0,0947	25,64
	5,3	1,668	1,8	3,002	2,781	3,24	2,078	-0,278	0,0772	15,43
	7,4	2,001	2,2	4,403	4,006	4,84	2,433	-0,233	0,0541	10,57
	9,6	2,262	2,6	5,881	5,116	6,76	2,709	-0,109	0,0119	4,20
	11,8	2,468	2,9	7,157	6,092	8,41	2,929	-0,029	0,0008	0,99
	14,5	2,674	3,3	8,825	7,151	10,89	3,148	0,152	0,0232	4,62
	18,7	2,929	3,8	11,128	8,576	14,44	3,418	0,382	0,1459	10,05
Итого	71,6	15,315	18,7	41,918	35,035	50,83	18,720	-0,020	0,5688	116,08
Среднее значение	8,95	1,914	2,34	5,240	4,379	6,35	–	–	0,0711	14,51
	–	0,846	0,935	–	–	–	–	–	–	–
	–	0,716	0,874	–	–	–	–	–	–	–

Найдем уравнение регрессии:

,

.

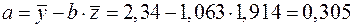Т.е. получаем следующее уравнение регрессии: . Теперь заполняем столбцы 8-11 нашей таблицы.

Индекс корреляции находим по формуле (1.21):

,

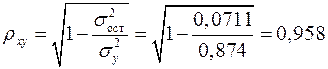а индекс детерминации , который показывает, что 91,8% вариации результативного признака объясняется вариацией признака-фактора, а 8,2% приходится на долю прочих факторов.

Средняя ошибка аппроксимации: , что недопустимо велико.

-критерий Фишера:

,

значительно превышает табличное .

Изобразим на графике исходные данные и линию регрессии:

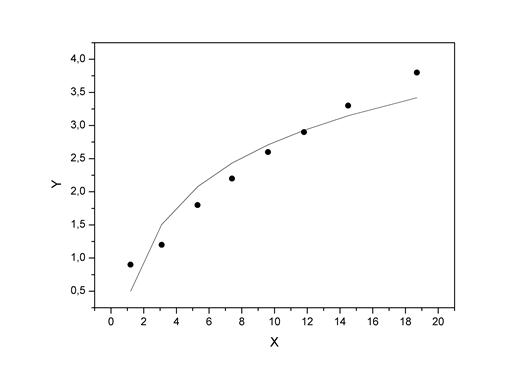
Рис. 1.6.

Для нахождения параметров регрессии 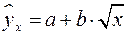делаем замену и составляем вспомогательную таблицу ().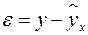

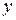
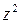
	1,2	1,10	0,9	0,99	1,2	0,81	0,734	0,166	0,0276	18,46
	3,1	1,76	1,2	2,11	3,1	1,44	1,353	-0,153	0,0235	12,77
	5,3	2,30	1,8	4,14	5,3	3,24	1,857	-0,057	0,0033	3,19
	7,4	2,72	2,2	5,98	7,4	4,84	2,247	-0,047	0,0022	2,12
	9,6	3,10	2,6	8,06	9,6	6,76	2,599	0,001	0,0000	0,05
	11,8	3,44	2,9	9,96	11,8	8,41	2,912	-0,012	0,0001	0,42
	14,5	3,81	3,3	12,57	14,5	10,89	3,259	0,041	0,0017	1,20
	18,7	4,32	3,8	16,43	18,7	14,44	3,740	0,060	0,0036	1,58
Итого	71,6	22,54	18,7	60,24	71,6	50,83	18,700	-0,001	0,0619	39,82
Среднее значение	8,95	2,82	2,34	7,53	8,95	6,35	–	–	0,0077	4,98
	–	1,00	0,935	–	–	–	–	–	–	–
	–	1,00	0,874	–	–	–	–	–	–	–

Найдем уравнение регрессии:

,

.

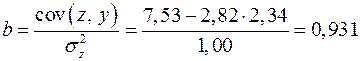Т.е. получаем следующее уравнение регрессии: . Теперь заполняем столбцы 8-11 нашей таблицы.

Индекс корреляции находим по формуле (1.21):

,

а индекс детерминации , который показывает, что 99,1% вариации результативного признака объясняется вариацией признака-фактора, а 0,9% приходится на долю прочих факторов.

Средняя ошибка аппроксимации: показывает, что линия регрессии хорошо приближает исходные данные.

-критерий Фишера:

,

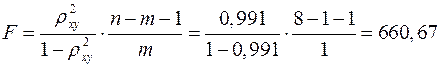значительно превышает табличное .

Изобразим на графике исходные данные и линию регрессии:

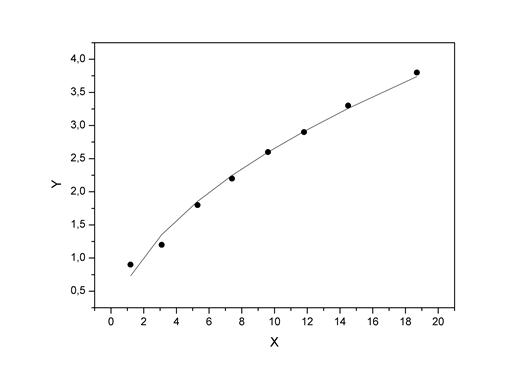
Рис. 1.7

Для нахождения параметров регрессии необходимо провести ее линеаризацию, как было показано выше:

,

где .

Составляем вспомогательную таблицу для преобразованных данных:

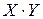
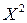
	0,182	-0,105	-0,019	0,033	0,011	0,8149	0,0851	0,0072	9,46
	1,131	0,182	0,206	1,280	0,033	1,3747	-0,1747	0,0305	14,56
	1,668	0,588	0,980	2,781	0,345	1,8473	-0,0473	0,0022	2,63
	2,001	0,788	1,578	4,006	0,622	2,2203	-0,0203	0,0004	0,92
	2,262	0,956	2,161	5,116	0,913	2,5627	0,0373	0,0014	1,43
	2,468	1,065	2,628	6,092	1,134	2,8713	0,0287	0,0008	0,99
	2,674	1,194	3,193	7,151	1,425	3,2165	0,0835	0,0070	2,53
	2,929	1,335	3,910	8,576	1,782	3,7004	0,0996	0,0099	2,62
Итого	15,315	6,002	14,637	35,035	6,266	18,608	0,0919	0,0595	35,14
Среднее значение	1,914	0,750	1,830	4,379	0,783	–	–	0,0074	4,39
	0,846	0,470	–	–	–	–	–	–	–
	0,716	0,221	–	–	–	–	–	–	–

Найдем уравнение регрессии:

,

.

Т.е. получаем следующее уравнение регрессии: . После потенцирования находим искомое уравнение регрессии:

.

Теперь заполняем столбцы 7-10 нашей таблицы.

Индекс корреляции находим по формуле (1.21):

,

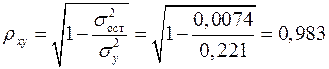а индекс детерминации , который показывает, что 96,7% вариации результативного признака объясняется вариацией признака-фактора, а 3,3% приходится на долю прочих факторов.

Средняя ошибка аппроксимации: показывает, что линия регрессии хорошо приближает исходные данные.

-критерий Фишера:

,

значительно превышает табличное .

Изобразим на графике исходные данные и линию регрессии:

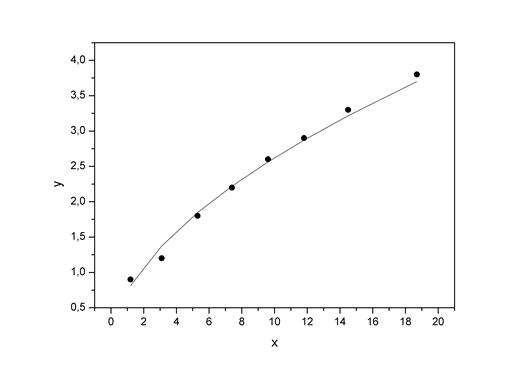
Рис. 1.8.

Сравним построенные модели по индексу детерминации и средней ошибке аппроксимации:

Таблица 1.8

Модель	Индекс детерминации, (, )	Средняя ошибка аппроксимации, , %
Линейная модель,	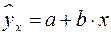0,987	6,52
Полулогарифмическая модель,	0,918	14,51
Модель с квадратным корнем,	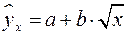0,991	4,98
Степенная модель,	0,967	4,39

Наиболее хорошо исходные данные аппроксимирует модель с квадратным корнем. Но в данном случае, так как индексы детерминации линейной модели и модели с квадратным корнем отличаются всего на 0,004, то вполне можно обойтись более простой линейной функцией.

Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Если же этим влиянием пренебречь нельзя, то в этом случае следует попытаться выявить влияние других факторов, введя их в модель, т.е. построить уравнение множественной регрессии

,

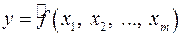где 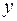– зависимая переменная (результативный признак), 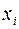– независимые, или объясняющие, переменные (признаки-факторы).

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целом ряде других вопросов эконометрики. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.