ТЕРМОДИНАМИЧЕСКИМИ ФУНКЦИЯМИ И ПАРАМЕТРАМИ
ВЗАИМОСВЯЗЬ ЭНЕРГИИ ГИББСА С ДРУГИМИ
1) подставив в уравнение (80) значение энтальпии 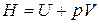 :
:
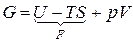 ,
,
получим:
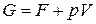 . (82)
. (82)
Для 1 моль идеального газа 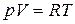 , следовательно
, следовательно
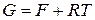 .
.
Из анализа последнего уравнения видно, что если идеальный газ взят при абсолютном нуле температур, то 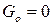 , а
, а 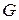 и
и 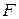 одинаковы.
одинаковы.
2) продифференцировав уравнение (82), получим:
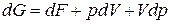 .
.
Так как 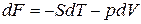 ,
,
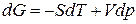 . (83)
. (83)
Поскольку 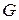 изменяется при изменении давления и температуры, т.е.
изменяется при изменении давления и температуры, т.е. 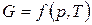 , то
, то 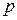 и
и 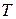 являются собственными параметрами состояния системы энергии Гиббса.
являются собственными параметрами состояния системы энергии Гиббса.
Если 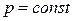 :
: 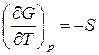 уравнение устанавливает связь
уравнение устанавливает связь 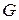 с
с 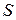 ;
;
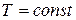 :
: 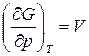 уравнение устанавливает связь
уравнение устанавливает связь 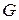 с
с 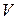 .
.
Таким образом, энергия Гиббса является характеристической функцией.
3) запишем уравнение (80) последовательно для исходного (1) и конечного (2) состояния системы в каком-либо изобарно-изотермическом процессе:
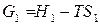 ;
; 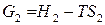 .
.
вычтем почленно из последнего уравнения предыдущее и получим вторую форму записи уравнения Гиббса – Гельмгольца:
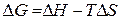 (84) Уравнение Гиббса – Гельмгольца, позволяющее определить возможность протекания изобарно-изотер-мического процесса (применяется чаще, чем первая)
(84) Уравнение Гиббса – Гельмгольца, позволяющее определить возможность протекания изобарно-изотер-мического процесса (применяется чаще, чем первая)
Перепишем уравнение Гиббса-Гельмгольца (83) в виде:
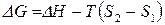 .
.
подставим в (83) вместо 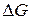 ,
, 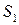 и
и 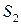 их значения:
их значения:
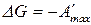 ;
; 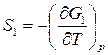 ;
; 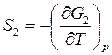 .
.
После подстановки, получим:
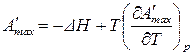 (85) уравнение максимальной работы Гиббса-Гельмгольца
(85) уравнение максимальной работы Гиббса-Гельмгольца
Когда 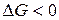
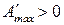
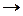 прямой ход реакции;
прямой ход реакции;
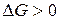
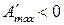
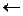 обратный ход реакции;
обратный ход реакции;
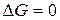
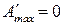
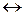 условие термодинамического равновесия в системе при
условие термодинамического равновесия в системе при 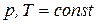 .
.
Вывод: есть пять критериев направления самопроизвольного протекания процессов и равновесия в системах (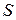 и 4 термодинамические потенциала)
и 4 термодинамические потенциала)
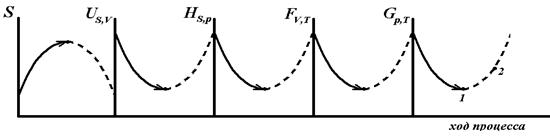
Рис. 9. Изменение энтропии 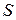 ,
, 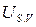 –,
–, 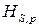 –,
–, 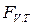 –,
–, 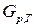 – потенциалов в ходе процесса:
– потенциалов в ходе процесса: 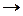 самопроизвольный процесс; --- – несамопроизвольный процесс
самопроизвольный процесс; --- – несамопроизвольный процесс
| Система | Условие самопроизвольного протекания процесса | Условие равновесия | Условие экстремума |
| Изолированная | 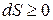
| 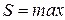 , , 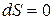
| 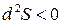
|
| Любая | 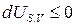
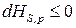
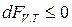
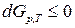
| 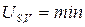 , , 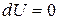
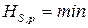 , , 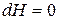
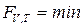 , , 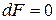
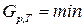 , , 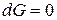
| 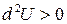
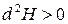
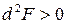
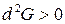
|
 2014-02-12
2014-02-12 271
271






