Метод Гаусса с выбором главного элемента

Begin

Begin

Begin

a[j,i]:= - a[j,i]/a[i,i];

b[j]:= b[j] + a[j,i]*b[i];

For k:= i+1 to N do

a[j,k]:= a[j,k] + a[j,i]*a[i,k];

end;

end;

{Обратный ход: последовательное нахождение корней }

x[N]:= b[N]/a[N,N];

For i:= N-1 downto 1 do

h:= b[i];

For j:= i+1 to N do

h:= h - x[j] * a[i,j];

x[i]:= h/a[i,i];

end;

Блок-схема алгоритма прямого хода классического метода Гаусса

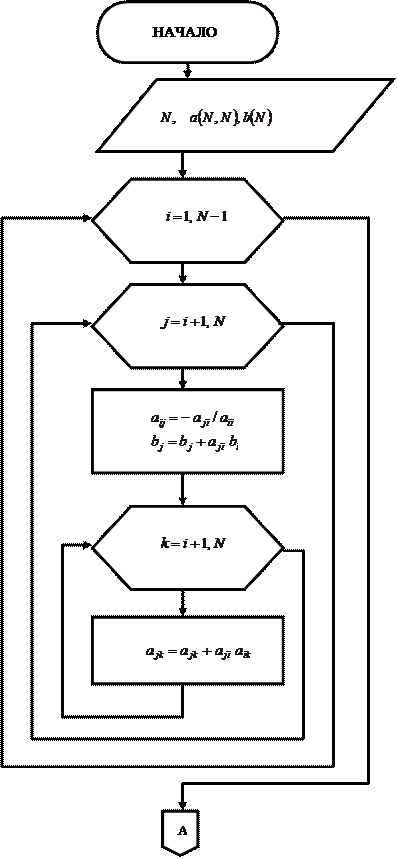
Рис. 1а. Прямой ход исключения классического метода Гаусса.
Блок-схема алгоритма обратного хода классического метода Гаусса

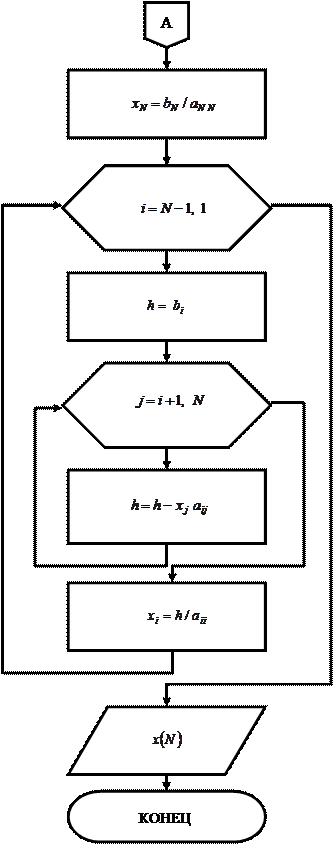
Рис. 1б. Обратной ход исключения классического метода Гаусса.

В заключении отметим, что классический метод Гаусса не применим, если в ходе расчёта на главной диагонали оказался нулевой элемент. Кроме того, если на главной диагонали оказался слишком маленький по значению элемент (мало отличим от нуля) и если эта строка умножается на большие числа, то это приводит к значительным ошибкам округления при вычитаниях, т.е. имеется большая потеря точности при значениях диагональных элементов, близких к нулю.

При реализации данного метода требуется:

· выполнить 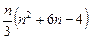арифметических операций, в том числе 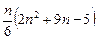умножений и делений;

· одновременно запоминать 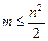промежуточных результатов.

Метод рекомендуется применять в тех случаях, когда:

· от решения требуется не очень высокая степень точности;

· прямой метод используется для получения начального приближения с последующим уточнением по итерационной схеме;

· требуется решить систему высокого порядка, у которой матрица коэффициентов имеет подавляющее количество нулевых элементов.

Современные исследования, относящиеся к гауссову исключению, вскрыли важность двух идей: необходимости выбора главного элемента и правильной интерпретации ошибок округления.

Метод Гаусса с выбором главного элемента (метод главных элементов) заключается в том, что при прямом ходе производится выбор наибольшего по модулю (главного) из всех элементов рассматриваемого столбца. Такая процедура называется выбором главного элемента столбца.

Последнее исключает деление на ноль, если матрица 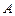содержит нулевые элементы, и повышает точность вычислений при наличии ошибок округления.

Количество арифметических операций в методе Гаусса связано с размерностью системы и примерно равно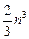. В методе Гаусса с выбором главного элемента погрешность округления обычно невелика. Только для плохо обусловленных систем устойчивость этого метода оказывается недостаточной.

Погрешность округления можно ещё уменьшить, если выбирать в каждом цикле элемент, максимальный по модулю во всей матрице. Однако точность при этом возрастает не сильно по сравнению со случаем выбора главного элемента, а расчёт заметно усложняется, ибо требуется перестановка не только строк, но и столбцов.

Контроль полученных решений можно провести путем их подстановки в исходную СЛАУ и вычисления невязок r _k, разностей между правыми и левыми частями уравнений:

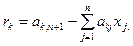
При малой погрешности решений величины r _k будут близки к нулю.