Вариант 2
Вариант 1
Применительно к СНАУ 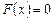 получим следующий алгоритм:
получим следующий алгоритм:
1. Выбрать начальный вектор 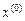 , положить
, положить 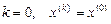
2. Вычислить вектор 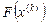 . Если все
. Если все 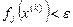 , где - заданная точность расчета, то получено решение, расчет окончен. Если
, где - заданная точность расчета, то получено решение, расчет окончен. Если 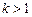 и
и 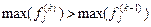 , то итерационный процесс расходится, расчет завершить аварийно.
, то итерационный процесс расходится, расчет завершить аварийно.
3. Построить матрицу Якоби
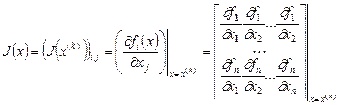
и вычислить значения всех производных в точке 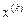 .
.
4. Решить систему уравнений, определив вектор поправок 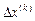
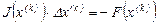
5. Вычислить новое приближение
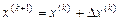
и положить 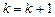 .
.
6. Если 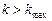 , где
, где 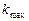 -заданное предельное число итераций, то аварийно завершить расчет, иначе перейти к п.2 алгоритма.
-заданное предельное число итераций, то аварийно завершить расчет, иначе перейти к п.2 алгоритма.
7. Конец алгоритма.
Метод Ньютона при начальном приближении близком к некоторому решению часто обладает устойчивой квадратичной сходимостью. При плохой начальной точке 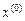 имеет место расходящийся итерационный процесс. Метод Ньютона расходится, если матрица Якоби плохо обусловлена в окрестности решения. Часто перед использованием метода Ньютона выполняют несколько итераций, например, методом последовательных приближений для того, чтобы иметь «хорошее» начальное приближение.
имеет место расходящийся итерационный процесс. Метод Ньютона расходится, если матрица Якоби плохо обусловлена в окрестности решения. Часто перед использованием метода Ньютона выполняют несколько итераций, например, методом последовательных приближений для того, чтобы иметь «хорошее» начальное приближение.
В качестве косвенного критерия расхождения итерационного процесса можно использовать изменение знака Якобиана - определителя матрицы Якоби. Однако это условие, являясь достаточным, не является необходимым. Якобиан может быть вычислен, как побочный продукт решения методом Гаусса системы из п.3 алгоритма.
Алгоритм:
- Задаём абсолютную или относительную погрешность
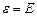 , число уравнений
, число уравнений 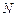 , максимальное число итераций
, максимальное число итераций 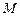 и вектор начальных приближений
и вектор начальных приближений 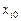 (с компонентами
(с компонентами 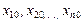 ).
). - Используя разложение
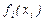 в ряд Тейлора, формулируем матрицу Якоби
в ряд Тейлора, формулируем матрицу Якоби 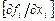 , необходимую для расчёта приращений
, необходимую для расчёта приращений 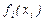 при малом изменении переменных. Матрица Якоби в развёрнутом виде записывается следующим образом:
при малом изменении переменных. Матрица Якоби в развёрнутом виде записывается следующим образом:
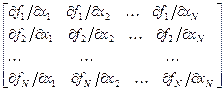
Поскольку аналитическое дифференцирование 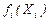 в общем случае нежелательно, заменяем частные производные в матрице Якоби их приближенными конечно-разностными значениями
в общем случае нежелательно, заменяем частные производные в матрице Якоби их приближенными конечно-разностными значениями
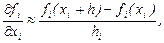
где 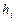 - малое приращение
- малое приращение 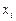 , например
, например 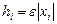 .
.
- Составляем и решаем систему линейных уравнений для малых приращений
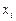 :
:
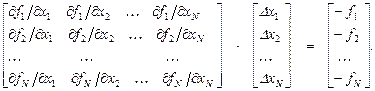
Решение этой системы даёт 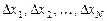 , т. е.
, т. е. 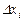 .
.
- Вычисляем уточнённые значения
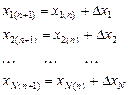
или в общем виде
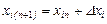
- Для всех
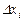 проверяем одно из условий:
проверяем одно из условий: 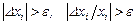 по абсолютной и относительной погрешностям.
по абсолютной и относительной погрешностям.
Если оно выполняется, идём к п. 2, т. е. выполняем новую итерацию. Иначе считаем вектор 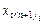 найденным решением.
найденным решением.
Испытаем метод Ньютона на примере
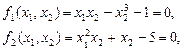
с 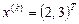 . Матрица Якоби имеет вид
. Матрица Якоби имеет вид
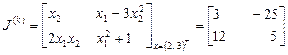 ,
,
и уравнение Ньютона имеет вид
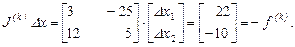
Использование гауссова исключения даёт 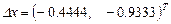 , и поэтому новым приближением к решению будет
, и поэтому новым приближением к решению будет 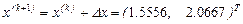 . Решением же системы нелинейных уравнений является
. Решением же системы нелинейных уравнений является 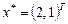 .
.
 2014-02-12
2014-02-12 674
674








