Begin
Begin
Begin
Begin
Begin
Begin
Пример 1.2
{Прямой ход исключения переменных}
For k:= 1 to N do
S:= a[k,k];
J:= k;
{Выбор главного элемента}
For I:= k+1 to N do
R:= a[i,k];
If Abs(R) > Abs(S) then
S:= R;
J:= i;
end;
end;
If S = 0.0 then Exit;
{Перестановка уравнений}
If j<>k then For I:= k to N do
R:= a[k,i];
a[k,i]:= a[j,i];
a[j,i]:= R;
end;
R:= b[k];
b[k]:= b[j];
b[j]:= R;
{Продолжение прямого хода}
For j:= k+1 to N do a[k,j]:= a[k,j]/S;
b[k]:= b[k]/S;
For i:= k+1 to N do
R:= a[j,k];
For j:= k+1 to N do a[i,j]:= a[i,j] - a[k,j]*R;
b[i]:= b[i] – b[k]*R;
end;
end;
{Обратный ход: последовательное нахождение корней }
If S <> 0.0 then
For i:= N Downto 1 do
S:= b[i];
For j:= i+1 to N do S:= S – x[j]*a[i,j];
x[i]:= S;
end;
При реализации данного метода требуется:
· выполнить 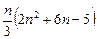 арифметических операций, в том числе
арифметических операций, в том числе 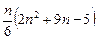 умножений и делений;
умножений и делений;
· одновременно запоминать 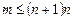 промежуточных результатов.
промежуточных результатов.
Метод главных элементов целесообразно применять в тех случаях, когда:
· коэффициенты системы являются дробными числами;
· решение должно быть получено с минимальной погрешностью;
· порядок системы 
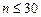 , а также когда необходимо решить систему высокого порядка, у которой матрица коэффициентов имеет подавляющее количество нулевых элементов.
, а также когда необходимо решить систему высокого порядка, у которой матрица коэффициентов имеет подавляющее количество нулевых элементов.
К недостаткам этого метода следует отнести громоздкость вычислительной схемы и сложность программирования.
Название метод Ньютона применяется к целому семейству методов, для которых собственно метод Ньютона служит базовым прототипом.
Рассмотрим простой пример.
Поскольку 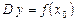 , где
, где 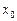 -начальное приближение, то
-начальное приближение, то 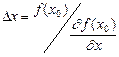
и можно получить новое приближение 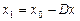 . Продолжая итерационный процесс можно с требуемой точностью приблизиться к одному из решений, например,
. Продолжая итерационный процесс можно с требуемой точностью приблизиться к одному из решений, например, 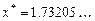
Расчетная формула для метода Ньютона может быть получена, если представить 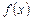 в окрестности текущего приближения
в окрестности текущего приближения 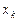 в виде ряда Тейлора
в виде ряда Тейлора
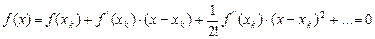 ,
,
и ограничиться линейными членами, тогда в матричной форме получим
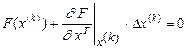 ,
,
где 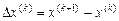
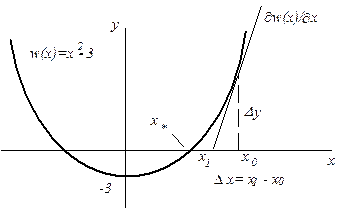
Рис. 1. Итерация метода Ньютона для 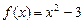 .
.
 2014-02-12
2014-02-12 1775
1775
