2014-02-12
1786
Для описания реальных физических процессов используются различные уравнения и методы описания. В качестве наиболее используемого и разработанного метода описания физических процессов в подземной гидромеханике применяется макроскопический метод, в основе которого лежит гипотеза сплошности, законы и методы механики сплошной среды.
В механике сплошных сред основными законами сохранения являются законы сохранения массы, изменения количества движения, изменения момента количества движения, энергии и баланса энтропии.
Однако законы сохранения выполняются для всех сплошных сред, а свойства сплошных сред могут быть различны. Поэтому для получения замкнутой системы уравнений кроме законов сохранения, описывающих физические процессы, добавляют определяющие уравнения и законы, которые задают особенности поведения.
В результате объединения законов сохранения и определяющих уравнений получается замкнутая система уравнений, в которой число уравнений равно числу неизвестных функций и которая определяет и задает математическую модель сплошной среды, описывающую конкретные физические процессы.
Для получения решения различных задач и описания конкретных физических процессов необходимо сделать постановку задачи, т.е. задать условия в начальный момент времени и условия на границах области пласта.
В результате имеем дифференциальные уравнения с начальными и граничными условиями, интегрируя которые можно определить распределение давления и скорости фильтрации по пласту в любой момент времени, т.е.
р = р(х, у, z, t), ωx = ωx (x, у, z, t), ωy= ωy(x, у, z, t), ωz= ωz(x, y, z, t).
Если рассматривается однородная несжимаемая жидкость (ρ = const) в недеформируемой пористой среде (m= const, k= const), то число искомых функций ограничивается только этими четырьмя функциями (р, ωx, ωy, ωz);
для фильтрации сжимаемого флюида в сжимаемой пористой среде кроме упомянутых функций нужно определить плотность ρ;
для более сложных процессов в число неизвестных функций включают вязкость μ, пористость m, проницаемость k. В этом случае нужно иметь восемь уравнений – дифференциальных и конечных - для определения восьми характеристик фильтрационного потока, жидкости и пористой среды.
Для подземной гидромеханики характерно изотермическое изменение параметров вследствие значительных величин удельной поверхности коллекторов и их теплоёмкости. Т.к. фильтрация представляет собой очень медленный процесс, то изменение температуры, возникающей в ходе движения, наличие сопротивления стенок поровых каналов и трещин, расширение флюида при уменьшении давления, успевает компенсироваться теплообменом с окружающими горными породами. Для таких изотермических процессов уравнение энергии рассматривать уже не нужно и ограничиватся уравнениями баланса массы (неразрывности) и движения.
Уравнение энергии необходимо рассматривать в локальных областях призабойной зоны из-за значительных перепадов давления, проявления дроссельного эффекта, а также при применении тепловых методов повышения нефте-газоотдачи.
Аналитическое решение системы дифференциальных уравнений удается получить лишь в ограниченном числе простейших очень сильно идеализированных случаев, например в задаче о притоке упругой жидкости к скважине в пласте бесконечной протяженности с постоянным дебитом. В более сложных случаях система уравнений решается численными методами с применением ЭВМ.
2.1.Закон сохранения массы.
Для математической формулировки законов сохранения рассматривают или материальный (подвижный), или контрольный объем.
Под материальным (подвижным) объемом понимается объем, состоящий во все моменты времени из одних и тех же материальных точек.
Область пространства, через границы которой могут проходить вещество, энергия, количество движения и т.д. и на которую могут действовать внешние силы, называется контрольным объемом, а поверхность, ограничивающая эту область – контрольной поверхностью. Контрольная поверхность может перемещаться в пространстве, но обычно считается неподвижной.
Вычислим массу флюида в контрольном объеме пористой среды. Масса жидкости, содержащаяся в бесконечно малом (физическом) объеме пористой среды, равна 
. Объем пор в элементарном объеме пористой среды равен 
. Умножив его на плотность, получим массу флюида в элементарном объеме пористой среды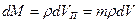 
Проинтегрировав написанное соотношение по всему контрольному объему, получим массу флюида в контрольном объеме
.
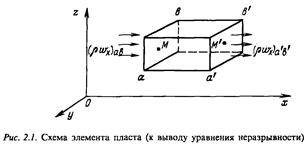
Так как через контрольную поверхность флюид может втекать и вытекать (рис. 2.1 На рис. ав и а'в' убрать, добавить нормаль), то масса флюида изменяется во времени. Изменение массы по времени вычисляется следующим образом.
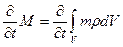
Изменение массы, равно притоку массы через контрольную поверхность, который равен
,
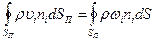где ni– внешняя нормаль к контрольной поверхности.
Поток массы через элементарную площадку dSравен скалярному произведению вектора массовой скорости и вектора нормали к площадке умноженному на ее площадь. Для того чтобы вычислить поток массы через всю поверхность нужно проинтегрировать эти элементарные потоки по всей поверхности. Следовательно, можно составить балансовое уравнение
= –
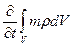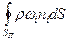. (2.1)
