2014-02-12
1871
Вывод дифференциального уравнения неустановившейся фильтрации
Для вывода дифференциального уравнения неустановившейся фильтрации используем уравнение неразрывности
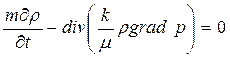или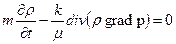 
Это уравнение справедливо только в том случае, если внутри объема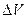 
нет источников или стоков, выделяющих или поглощающих флюид, не происходит химических реакций, фазовых превращений и т.д.
Дальнейшее преобразование связано с введением функцию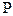
(функции Лейбензона),
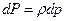или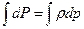 
или Р = const (2.16)
Равенство (2.16) позволяет определить явный вид функции Лейбензона при заданном уравнении состояния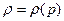 
Математическая модель фильтрации сжимаемой жидкости (газа) в недеформируемой изотропной пористой среде, без учета силы тяжести будет:
, 
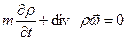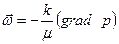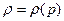, (2.14)
После введения функции Лейбензона систему (2.14) можно представить в виде
, 
, 
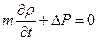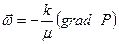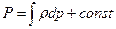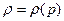, (2.15)
Замкнутые системы (2.14) и (2.15) представляют математическая модель фильтрации вязкой сжимаемой жидкости (газа) в недеформируемой изотропной пористой среде. Описывают неустановившееся фильтрационное течение.
Для установившегося процесса системы упрощаются
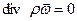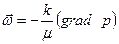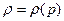, , (2.16)
и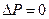 
, 
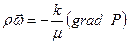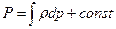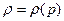, , (2.17)
При установившейся фильтрации первое уравнение системы (2.17) представляется уравнением Лапласа для функции Лейбензона, интегрируя которое можно найти функцию Лейбензона и затем определить распределение скорости и давление в пласте.
Первое уравнение системы (2.15) содержит две неизвестные функции - плотность и функцию Лейбензона, но при задании уравнений состояния (последнее уравнение в системе) его можно представить в виде дифференциального уравнения только для функции Лейбензона.
Если пласт считается деформируемым, пористость и проницаемость полагаются функциями давления, при этом изменение давление в пласте существенно, что вязкость тоже полагается функцией давления, то подставляя закон Дарси в уравнение неразрывности, получим
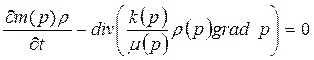(37)
тогда дифференциал функции Лейбензона равен:
,
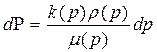тогда
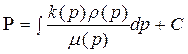, (2.20)
Тогда систему можно представить в виде
, 
,
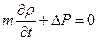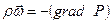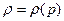, проницаемость
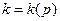, пористость 
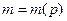, вязкость 
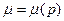(2.21)
