Основные понятия
Введение
Логика высказываний
Заключение
В качестве моделей графы удобно использовать в тех случаях, когда рассматриваются системы каких-либо объектов, между которыми существуют определенные связи а также в тех случаях, когда изучается структура системы, возможности ее функционирования.
В информатике графы используются в следующих разделах:
- алгоритмизация;
- структуры данных;
- моделирование и др.
Алгебра логики (логика высказываний) – это раздел дискретной математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними.
Алгебра логики возникла в середине 19 в. в трудах Дж. Буля и развивалась затем в работах Ч. Пирса, П. С. Порецкого, Б. Рассела, Д. Гильберта и др. Создание алгебры логики представляло собой попытку решать традиционные логические задачи алгебраическими методами.
С появлением теории множеств (70-е гг. 19 в.), поглотившей часть первоначального предмета алгебры логики, и дальнейшим развитием математической логики (последняя четверть 19 в. - 1-я половина 20 в.) предмет алгебры логики значительно изменился. Основным предметом алгебры логики стали высказывания.
В формально-логических выводах используются истинные и ложные предложения.
Определение: повествовательное предложение, о котором можно однозначно сказать, истинно оно или ложно, называется высказыванием.
Примеры высказываний: "кит - животное", "все углы - прямые" и т. п. Первое из этих высказываний является, очевидно, истинным, а второе - ложным. Предложение "реши задачу", также как и "2+2", не является высказываем.
Определения математических понятий не являются высказываниями, т.к. это принятые соглашения.
Будем обозначать высказывания большими латинскими буквами: A, B, C,….
Элементарные, нерасчленяемые высказывания будем называть атомами.
Употребляемые в обычной речи логические связки "и", "или", "если..., то...", "эквивалентно", частица "не" и т. д. позволяют из уже заданных высказываний строить новые, более "сложные" высказывания.
Аналогично тому, как в языке из простых предложений с помощью логических связок образуются сложные предложения, так и в логике высказываний из атомов можно образовывать составные высказывания.
Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями.
Рассмотрим определения логических операций, соответствующих логическим связкам.
Каждому высказывания можно сопоставить его истинностное значение, обозначаемое соответственно через И (если высказывание истинно), Л (если высказывание ложно).
Истинностное значение сложных высказываний зависит от истинностных значений высказываний, составлявших слоеное высказывание.
Эта зависимость устанавливается в данных ниже определениях я стращается в таблицах истинности.
Пусть A, В - произвольные высказывания, относительно которых не предполагается, что известно их истинностные значения.
Связке "НЕ" соответствует логическая операция отрицания, обозначение операции – знак ù или  .
.
Определение. Отрицанием высказывания A называется высказывание 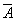 (ùA), которое истинно, если A – ложно, и ложно, если A – истинно.
(ùA), которое истинно, если A – ложно, и ложно, если A – истинно.
Таблица истинности отрицания:
| A | 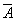 |
| И | Л |
| Л | И |
Пример: A: 2*2=4 – истинное высказывание; 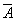 :
: 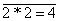 или 2*2
или 2*2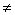 4 - ложное высказывание.
4 - ложное высказывание.
Связке "И" соответствует операция конъюнкция, обозначение операции – знак 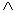 (или &).
(или &).
Определение. Конъюнкцией высказываний A и B называется высказывание A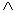 B (читается "A и B"), которое истинно тогда и только тогда, когда A, B – истинно.
B (читается "A и B"), которое истинно тогда и только тогда, когда A, B – истинно.
Таблица истинности конъюнкции:
| A | B | A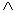 B B |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
Пример: A: 5 – нечетное число; B: Пушкин родился в 1799 г – истинные высказывания; поэтому высказываниеA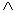 B: 5 – нечетное число
B: 5 – нечетное число 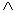 Пушкин родился в 1799 г. – истинное высказывание.
Пушкин родился в 1799 г. – истинное высказывание.
Связке "ИЛИ" соответствует операция дизъюнкция, обозначение операции – знак 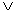 .
.
В формально-логических выводах «или» употребляется не в исключающем смысле (в отличие от обыденной речи, где эта связка может употребляться и в исключающем смысле и в неисключающем смысле)
Определение. Дизъюнкцией высказываний A и B называется высказывание A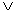 B (читается "A или B"), которое ложно тогда и только тогда, когда A, B – ложны.
B (читается "A или B"), которое ложно тогда и только тогда, когда A, B – ложны.
Таблица истинности дизъюнкции:
| A | B | A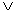 B B |
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
Пример. A: 7<10, и.в. В: 3 - число четное, л.в. A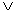 B: 7<10
B: 7<10 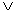 3 - число четное, и.в.
3 - число четное, и.в.
Связке "ЕСЛИ....ТО" соответствует логическая операция импликация, обозначение операции знак →.
Определение. Импликацией высказываний A и B называется высказывание A→B (читается "если A, то B"), которое ложно тогда и только тогда, когда A – истинно, а B – ложно.
Таблица истинности импликации:
| A | B | A→B |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
Пример. A: 2*2=5, л. в. В: 2=2, и. в. A→B: 2*2=5→ 2=2. и. в.
Высказывание A называется условием или посылкой, высказывание В - заключением или следствием импликации.
Связке "ТОГДА И ТОЛЬКО ТОГДА, КОГДА" соответствует операция эквиваленция, обозначение операция – знак «.
Определение. Эквиваленцией высказываний A и В навивается высказывание, обозначаемое A«B (читается:"A тогда и только тогда, когда В" или короче: "A эквивалентно В"), которое считается истинным только тогда, когда оба высказывания A и В имеют одинаковое истинностное значение.
Эквивалентность А«В читается также следующим образом: "Для того, чтобы A, необходимо и достаточно, чтобы В".
Таблица истинности эквиваленции:
| A | B | A«B |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | И |
Пример. A: 7 – число простое; и.в. В: в равнобедренном треугольнике при основании углы равны, и.в. A«В - и.в.
 2014-02-12
2014-02-12 756
756







