Метод отсечения Гомори

Алгоритм метода Гомори для решения полностью цело­численной задачи линейного программирования. Рассмот­рим полностью целочисленную задачу линейного програм­мирования:

,

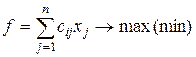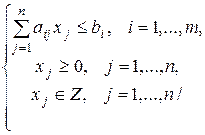
Алгоритм Гомори состоит из следующих этапов.

1. Решается ЗЛП с отброшенным условием целочисленности.

2. Полученное оптимальное решение (если оно сущест­вует) проверяется на целочисленность. Если условие целочисленности выполняется по всем переменным, то оптимальное решение целочисленной задачи совпадает с оптимальным решением ЗЛП. Если это условие не выполняется хотя бы по одной переменной, то переходят к третьему этапу. Если ЗЛП оказывается неразрешимой, то целочисленная задача тоже не имеет решения.

3. Строится дополнительное ограничение, отсекающее часть области, в которой содержится оптимальное решение ЗЛП и не содержитсяни одногодопустимого решения целочисленной задачи.

4. Последний этап предусматривает возвращение к ЗЛП с отброшенным условием целочисленности, но с рас­ширенной системой ограничений, в которую включено до­полнительное ограничение, полученное на третьем шаге. К расширенной системе ограничений вновь применяется симплексная процедура. Если найденное таким образом решение будет опять нецелым, то формируется новое до­полнительное ограничение и процесс вычислений повто­ряется.

Алгоритм Гомори позволяет за конечное число шагов прийти к оптимальному целочисленному решению, если оно существует.

С геометрической точки зрения каждому дополнитель­ному линейному ограничению в п -мерном пространстве соответствует определенная гиперплоскость, отсекающая от многогранника решений некоторую его часть, включая и оптимальную на данном этапе нецелочисленную верши­ну. При этом все точки с целочисленными координатами, в том числе и искомая оптимальная, остаются в усеченном многограннике. Так как множество целых точек усеченного многогранника совпадает с множеством целых точек исходного многогранника, то понятно, что если оптимальное решение ЗЛП на усеченном многограннике удовлетворяет условию целочисленности, то оно является оптимальным целочисленным решением и исходной задачи. Через несколько операций отсечения искомая целочисленная точка оказывается сначала на границе, а затем становится оптимальной вершиной неоднократно усеченного многогранника решений.

Может оказаться, что многогранник решений не содержит ни одной целочисленной точки. В этом случае, сколько бы ни вводили дополнительных ограничений, целочисленного допустимого решения получить нельзя.

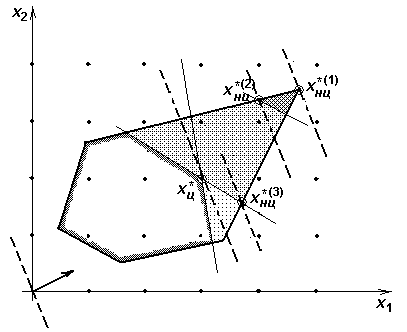
Для лучшего понимания существа вопроса обратимся к наглядной иллюстрации случая п =2 (рис. 4.2). Ограничения задачи определяют на плоскости некоторый многоугольник М, в вершине х *⁽¹⁾ которого, если не учитывать условия целочисленности, достигается максимум целевой функции. Внутри этого многоугольника имеется конечное множество точек, которым соответствуют решения с целочисленными значениями переменных (на рисунке они обозначены кружочками). На рисунке показаны три прямые, соответствующие трем дополнительным линейным ограничениям. Каждая из прямых отсекает часть области допустимых решений. Так, после отсечения части области прямой оптимальной оказывается вершина х *⁽²⁾, затем х *⁽³⁾, и, наконец, оптимальной становится цело­численная вершина х *.

Основное в алгоритме – составле­ние дополнительного ограничения, т. е. отсекающей ги­перплоскости, которая называется правильным отсечени­ем. Правильное отсечение должно удовлетворять следую­щим условиям: 1) быть линейным; 2) отсекать найденное оптимальное нецелочисленное решение ЗЛП; 3) не отсекать ни одной из целочисленных точек целочисленной задачи.