Метод дифференцирования.
При использовании данного метода повышения динамической точности АСК система снабжается дополнительным устройством, способным получать производные от измеряемого параметра.
Если подобраны производные нужного порядка, то можно подобрать такие коэффициенты, которые будут пропорциональны коэффициентам при дифференциальных членах того же порядка уравнения движения (4.1). Тогда
y» k2x(t) (4.3)
Так как уравнение движения (4.3) имеет алгебраический вид, динамические погрешности можно считать отсутствующими (или, более точно, пренебрежимо малыми, так как в уравнении нет точного равенства).
Данный метод реализуется следующим образом.
Динамические звенья системы, поведение которых описывается дифференциальными уравнениями, охватывают обратными связями. Тогда на вход каждого звена поступают сигналы, пропорциональные выходной величине и ее производным.
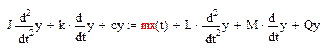 |
Так, если на вход исполнительного элемента АСК подать сигналы, пропорциональные измеряемой величине и ее производным, то уравнение движения (4.1) принимает вид
(4.4)
Или, если перегруппировать его члены и считать, что р - оператор дифференцирования
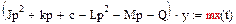 |
(4.5)
Теперь предлагается подобрать конструктивные параметры исполнительного элемента (J, k, с) и параметры обратной связи (L, M, Q) так, чтобы выполнялось равенство
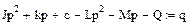 |
(4.6)
Здесь q - коэффициент пропорциональности.
Если это выполнимо, то уравнение движения (4.4) легко сводится к алгебраическому виду и, таким образом, динамические погрешности АСК можно считать отсутствующими.
 2014-02-12
2014-02-12 731
731







