В настоящее время на территории России существует обширная сеть геометрического нивелирования разных классов. По размерам и точности определения отметок реперов она по утверждению научного руководства ЦНИИГАиК не имеет равных во всём мире. Установлены 4 класса точности нивелирных сетей: I класс, II класс, III класс и IV класс. Ошибки измерения превышений по классам точности нивелирования приведены в таблице 1.2.
Нивелирование с предельной ошибкой 50 мм на 1 км хода называют техническим нивелированием, а с ошибкой 70 мм – инженерно-техническим.
Ошибки измерения превышений в государственном нивелировании Таблица 1.2
| N: п/п | Параметры точности | К Л А С С Ы Н И В Е Л И Р О В А Н И Я | |||
| I | II | III | IY | ||
СКО измер. превышения на 1 км хода (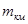 ) Предельная ошибка на 1 км хода ) Предельная ошибка на 1 км хода 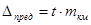 Значение t Значение t | 0,8 мм 3 мм 3,75 | 2,0 мм 5 мм 2,5 | 5,0 мм 10 мм 2,0 | 10,0 мм 20 мм 2,0 |
Нивелирные сети III и IY классов относятся к высотным сетям сгущения; они создаются внутри полигонов высшего класса (I или II) как отдельными линиями (ходами), так и в виде систем линий (ходов); при этом и отдельные линии и системы линий должны опираться не менее, чем на 2 репера высшего класса. Периметр полигонов в нивелировании III класса для обжитых районов составляет 60-150 км, для малообжитых районов 100-300 км, для городов 25-40 км. В сетях IY класса периметр полигонов составляет для обжитых районов 20-60 км, для необитых районов 25-80 км, для городов 8-12 км.
Периметры полигонов нивелирования III и IV классов Таблица 1.3
| Класс нивелирования | Населённые пункты | Обжитая местность | Необжитая местность |
| III | 25 – 40 км | 60 – 150 км | 100 – 300 км |
| IV | 8 – 12 км | 20 – 60 км | 25 – 80 км |
Линии нивелирования III и IY классов закрепляются на местности реперами не реже, чем через 5 км (в труднодоступных районах через 7 км). Каждый репер должен иметь индивидуальный номер, не повторяющийся как на данной линии, так и на ближайших линиях. Местоположение реперов отмечают на карте масштаба 1:25000 и крупнее, а также на аэроснимках, и определяют их географические координаты с точностью 10-15 дуговых секунд (200 – 300 м по широте и 300 – 450 м по долготе). На каждый репер составляют абрис и дают описание его местоположения. Кроме того, расположение всех реперов показывают на карте масштаба 1:100000, и эту карту впоследствии прикладывают к материалам нивелирования.
Если нивелирование III класса выполняется в горной местности (а для нивелирования I и II классов обязательно), то в измеренные превышения вводятся поправки за переход к системе нормальных высот.
Все работы по проложению нивелирных линий выполняют по утверждённым проектам.
В процессе любых геодезических измерений можно выделить 5 составляющих (пять аспектов):
- объект измерения,
- субъект измерения (исполнитель, наблюдатель, оператор и т.п.),
- методика измерений, реализующая достижения теории; методика измерений разрабатывается для каждого вида измерений и должна обеспечивать наибольшую эффективность при наименьших затратах;
- различного рода помехи, в частности, внешние условия, при которых выполняются измерения.
При переходе к измерениям более высокой точности приходится:
- более тщательно готовить объект измерений к процессу измерений,
- подбирать более точный измерительный прибор и выполнять его поверки и исследования,
- готовить кадры для точных и высокоточных измерений,
- разрабатывать и применять более совершенную методику измерений,
- более тщательно учитывать влияние внешних условий и другие помехи,
- применять более строгие способы математической обработки измерений с обязательной оценкой точности результатов обработки.
Объектом нивелирования является превышение между точками, зафиксированными на местности центрами реперов; именно это превышение и нужно измерить в процессе прокладки нивелирных линий. Перед началом работы следует опознать реперы со 100%-ной надёжностью и сделать их доступными для постановки нивелирных реек (откопать центры и устранить все помехи). Нужно выполнить также рекогносцировку линии нивелирования, выбрать наиболее простой её вариант и, если можно, наметить места постановки нивелира и реек.
СИСТЕМЫ ВЫСОТ В ГОДЕЗИИ.
Классификация систем высот
Одна из основных задач геодезии – изучить действительную (физическую) поверхность Земли. Изучить поверхность Земли, то есть определить положение любой её точки в принятой системе координат. Как известно, в геодезии применяются различные системы координат: 1) геодезические широта B и долгота L на поверхности эллипсоида и высота H точки над поверхностью эллипсоида; 2) прямоугольные координаты x и y в проекции Гаусса и высота H над поверхностью эллипсоида; 3) прямоугольные пространственные координаты X,Y,Z. Таким образом, высота точек земной поверхности – это одна из координат, определяющих фигуру Земли относительно исходной отсчётной поверхности (поверхности референц-эллипсоида или общего земного эллипсоида); высота точки определяет расстояние точки от эллипсоида по нормали к нему.
Требования к определению высот точек и превышений между отдельными точками колеблются в очень широких пределах в зависимости от целей использования высот. Для изображения рельефа на топографических картах и планах высоты точек нужно определять с относительно невысокой точностью – порядка сантиметров и десятков сантиметров. Но для проектирования и строительства различных инженерных сооружений или при изучении вертикальных смещений блоков земной коры или отдельных элементов сооружения высоты точек и их разности нужно определять с точностью миллиметров и даже долей миллиметра. Понятно, что такие точности могут быть обеспечены только при теоретически строгом решении проблем измерения превышений и вычисления высот точек.
Однако, долгое время вопрос о точном вычислении высот не был решён с необходимой строгостью; вплоть до середины 20-го столетия существовали лишь приближённые решения этих проблем. И только в исследованиях советского учёного М.С. Молоденского и его соратников и учеников А.А. Изотова, В.Ф. Еремеева, М.И. Юркиной, работавших в ЦНИИГАиКе, дано полное и строгое решение проблемы высот. Теория систем высот основывается на теории гравитационного поля Земли, то есть, на теории поля силы тяжести. Это поле потенциальное, то есть, в каждой точке пространста на поверхности Земли и вблизи её потенциал силы тяжести имеет конкретное числовое значение. Разность потенциалов двух точек – это работа, которую нужно совершить, чтобы переместить единичную массу из одной точки поля в другую; работа может либо высвобождаться, либо затрачиваться, смотря по знаку разности потенциалов точек
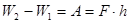 ; (1.1)
; (1.1)
Сила притяжения F выражается формулой
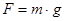 ,
,
где g – ускорение силы тяжести Земли, используя которую, можно переписать формулу (1) при единичной массе (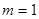 )
)
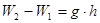 .
.
В соответствии с разностью потенциалов определяется превышение между точками
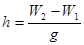 ,
,
или
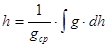 , (1.2)
, (1.2)
так как 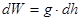 .
.
В этих формулах W2 и W1 – потенциал силы тяжести в точках 2 и 1; gср – среднее значение ускорения силы тяжести на пути от точки 1 к точке 2; h – превышение между точками.
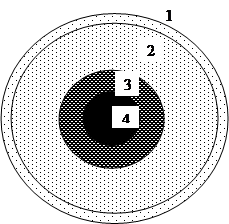
Из непосредственных измерений получают превышения между точками стояния нивелира, а точнее – расстояние между уровенными поверхностями точек установки реек. Поскольку уровенные поверхности, строго говоря, не параллельны одна другой, то измеренное превышение между точками 2 и 1, равное сумме превышений на станциях по ходу от точки 1 к точке 2, нельзя отнести к какой-либо системе высот. Если бы Земля состояла из концентрических слоёв и внутри каждого слоя плотность была бы постоянной, то уровенные поверхности были бы параллельны и сумма превышений, измеренных на станциях, была в точности равна превышению между точками 2 и 1. Известно, что Земля примерно так и устроена; в первом приближении выделяют земную кору (1), мантию (2), ядро (3) и субъядро (4), и плотность вещества внутри каждого из этих слоёв считается примерно постоянной, а от слоя к слою изменяется (рис.1.1).
В реальной Земле уровенные поверхности не параллельны как вследствие того, что массы различной плотности распределены в теле Земли неравномерно и хаотично, так и вследствие того, что гравитационное поле земли неоднородно; замечено, что на экваторе расстояние между уровенными поверхностями меньше, а ближе к полюсам - больше (рис.1.2).
Непосредственно измеренные превышения зависят от пути нивелирования из-за непараллельности уровенных поверхностей.
Если идти по пути от точки О до точки К и затем по уровенной поверхности КМ (рис.1.2), то 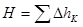 (рис.1.2); если же идти сначала по уровенной поверхности ОМ1 и затем по пути М1М, то
(рис.1.2); если же идти сначала по уровенной поверхности ОМ1 и затем по пути М1М, то 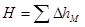 . Но
. Но 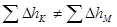 и потому высота точки М неопределённа, а в ходе по замкнутому контуру сумма превышений не будет равна нулю.
и потому высота точки М неопределённа, а в ходе по замкнутому контуру сумма превышений не будет равна нулю.
Непосредственно измеренные превышения, «привязанные» к отвесным линиям на каждой точке установки реек, зависят также от аномальностей силы тяжести. Такая неопределённость измеренных превышений заставляет применять специально разработанные системы высот.
 | |||
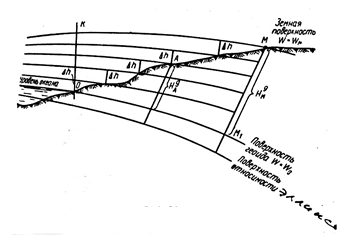 | |||
Рисунок 1.1 Рисунок 1.2
Согласно теории Молоденского геодезические высоты точек земной поверхности следует получать как сумму двух слагаемых: расстояния от референц-элипсоида до поверхности квазигеода и расстояния от квазигеоида до соответствующей точки земной поверхности; оба этих отрезка должны быть расположены по нормали к поверхности референц-эллипсоида.
Вообще-то, почти так же считали и раньше: геодезическую высоту получали как сумму двух отрезков: расстояния от референц-эллипсоида до поверхности геоида и расстояния от геоида до земной поверхности. Но в этом случае началом счёта высот от «уровня моря» является поверхность геоида, которая, как было доказано многими учёными, не может быть строго определена без знания распределения масс различной плотности внутри Земли. В теории Молоденского роль такой поверхности выполняет поверхность квазигеоида, которая однозначно определяется только по наземным измерениям. В этом одно из основных отличий теории Молоденского от предыдущих теорий (рис.1.3)
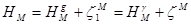 . (1.3)
. (1.3)
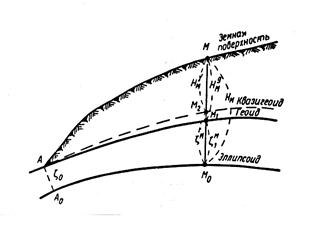
Рисунок 1.3
Оба слагаемых в формуле (1.3) - высота точки М над поверхностью геоида плюс высота геоида над эллипсоидом и высота точки М над поверхностью квазигеоида плюс высота квазигеоида над эллипсоидом, - должны измеряться по нормали к эллипсоиду. В первом случае (ортометрические высоты) уровнем моря, от которого считаются высоты, считается поверхность геоида, во втором случае (нормальные высоты) – поверхность квазигеоида.
Какую систему выбрать? Система ортометрических высот применялась в СССР до Молоденского; в некоторых странах она применяется и сейчас. Но в России после работ Молоденского перешли на систему нормальных высот. В последние 3 – 5 лет спор о том, от чего считать высоты – от геоида или от квазигеоида, - опять обострился. Из соратников Молоденского в живых осталась лишь М.И. Юркина (она за квазигеоид); за геоид выступал М.М. Машимов (он скончался в 2001 году). Спор вёлся в журнале «Геодезия и картография» в 1998 – 2001 годах.
Существуют четыре системы геопотенциальных высот: приближённые высоты, ортометрические высоты, нормальные высоты и динамические высоты.
Приближённые высоты
Приближённые высоты получатся, если не принимать во внимание реальное гравитационное поле силы тяжести Земли
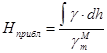 , (1.4)
, (1.4)
где 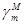 - среднее значение нормальной силы тяжести на отрезке ММ1.
- среднее значение нормальной силы тяжести на отрезке ММ1.
Приближённые высоты вычисляют тогда, когда вдоль линии нивелирования не производились измерения силы тяжести, и они являются промежуточными при вычислении высот точек в других системах. Чтобы получить приближённые высоты, нужно исправить измеренные превышения только за непараллельность уровенных поверхностей
Ортометрические высоты
Ортометрическая высота – это расстояние от поверхности геоида до точки земной поверхности, считаемое по отвесной линии, проходящей через точку
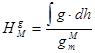 . (1.5)
. (1.5)
Ортометрические высоты не зависят от пути нивелирования, но точки, расположенные на одной уровенной поверхности, могут иметь разные ортометрические высоты, что неудобно при выполнении некоторых геодезических работ. Причиной тому служит тот факт, что расстояния от геоида до уровенной поверхности не остаются постоянными, а изменяются в зависимости от действительных значений силы тяжести на отвесной линии ММ1 (от точки поверхности Земли до геоида). Ортометрические высоты имеют крупный теоретический недостаток – они не могут быть вычислены точно, так как оба слагаемых в формуле для HМ согласно теории гравитационного поля Земли являются приближёнными числами
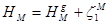 ; (1.6)
; (1.6)
здесь 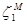 - высота геоида над эллипсоидом в точке M, HM означает геодезическую высоту (высоту точки над эллипсоидом).
- высота геоида над эллипсоидом в точке M, HM означает геодезическую высоту (высоту точки над эллипсоидом).
Нормальные высоты
Нормальная Земля – теоретическая модель Земли в виде эллипсоида вращения с полуосями a и b и массой М такими, что при его вращении с угловой скоростью w, равной скорости вращения Земли, значение нормального потенциала на его поверхности есть величина постоянная. Поверхность такого эллипсоида называют также уровенным эллипсоидом.
Нормальные высоты (рис.5) не зависят от пути нивелирования. Точки, расположенные на одной уровенной поверхности, имеют в общем случае неодинаковые нормальные высоты, кроме случая, когда точки располагаются на одной параллели (то есть, имеют одинаковую широту).
Геодезическая высота точки (от поверхности эллипсоида) складывается из нормальной высоты (высоты над поверхностью квазигеоида) и аномалии высоты (высоты квазигеоида над поверхностью эллипсоида)
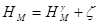 ; (1.7)
; (1.7)
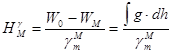 - нормальная высота;
- нормальная высота;
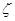 - аномалия высоты;
- аномалия высоты; 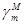 -среднее значение нормальной силы тяжести;
-среднее значение нормальной силы тяжести;
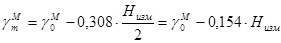 ;
;
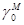 - нормальное значение силы тяжести на эллипсоиде; оно является функцией широты точки.
- нормальное значение силы тяжести на эллипсоиде; оно является функцией широты точки.
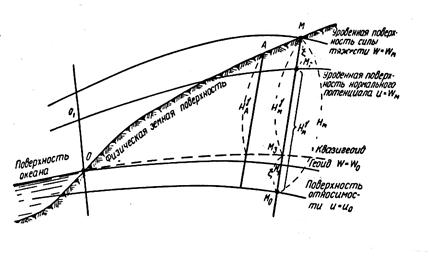
Рис. 1.4
Строгая формула для вычисления нормальной силы тяжести (формула Сомильяни) имеет вид
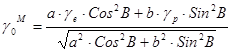 ,
,
но для практических вычислений применяют более удобную формулу
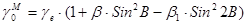 ;
;
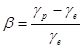 ;
; 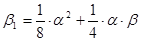 ;
;
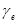 - нормальное значение силы тяжести на экваторе;
- нормальное значение силы тяжести на экваторе;
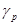 - нормальное значение силы тяжести на полюсе;
- нормальное значение силы тяжести на полюсе;
a - сжатие эллипсоида.
Для получения нормального превышения нужно исправить измеренное превышение по формуле
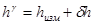 , (1.8)
, (1.8)
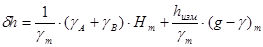 . (1.9)
. (1.9)
Динамические высоты
Тот факт, что нормальные и ортометрические высоты точек одной уровенной поверхности неодинаковы, делает их неудобными при строительстве крупных инженерных сооружений. Действительно, на Рыбинском водохранилище разность нормальных высот южного и северного участков воды равняется 8 мм, на озере Севан – 88 мм, на озере Байкал – 165 мм и так далее.
Если при строительстве крупной оросительной системы использовать нормальные высоты, то может оказаться, что вода потечёт совсем не туда, куда нужно. В этом и других подобных случаях применяют динамические высоты. Динамическая высота получается, если в формуле высоты используется нормальное значение силы тяжести, одинаковое для всех точек строящегося сооружения; конкретно таким значением принимают нормальное значение силы тяжести на широте 450 (по Гельмерту 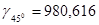 гл).
гл).
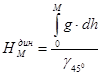 . (1.10)
. (1.10)
или
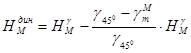 . (1.11)
. (1.11)
Динамические высоты для всех точек уровенной поверхности одинаковы.
ЛЕКЦИЯ 2. ВЛИЯНИЕ КРИВИЗНЫ И РЕФРАКЦИИ НА ИЗМЕРЯЕМОЕ ПРЕВЫШЕНИЕ.
Высота точки является одной из её координат; она определяет положение точки по высоте относительно поверхности референц-эллипсоида; высоты всех точек поверхности Земли определяют фигуру Земли в целом. Высоты точек считаются «от уровня моря», роль которой может выполнять либо поверхность геоида (система ортометрических высот), либо поверхность квазигеоида (система нормальных высот). Поскольку ни та, ни другая поверхность на местности не обозначены, для вычисления высоты точки существует лишь один вариант: считать известной высоту 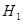 одной точки, измерить превышение h другой точки относительно первой точки и вычислить высоту второй точки
одной точки, измерить превышение h другой точки относительно первой точки и вычислить высоту второй точки 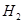 по формуле
по формуле
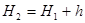 . (2.1)
. (2.1)
Все четыре системы высот (приближённые высоты, ортометрические высоты, нормальные высоты и динамические высоты) являются моделями по отношению к объективно существующей реальности, которая заключается в том, что на местности можно зафиксировать и использовать только одно направление – направление силы тяжести; отвес фиксирует отвесное (вертикальное) направление, а ось цилиндрического уровня – горизонтальное направление.
Для измерения превышений с помощью горизонтального луча визирования применяется нивелир и две рейки; у нивелира визирная линия трубы в моменты измерений занимает горизонтальное положение, а рейки устанавливаются вертикально в точках 1 и 2. Измеренное с помощью нивелира превышение h является расстоянием между двумя уровенными поверхностями, проведёнными через точки установки реек: задней и передней. Отсчёт по задней рейке обозначается a, по передней – b; если считать уровенные поверхности горизонтальными плоскостями, а направления силы тяжести в точках 1 и 2 считать параллельными, то превышение между точками 1 и 2 выразится простой формулой (2.2)
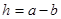 . (2.2)
. (2.2)
Во втором приближении будем считать уровенные поверхности сферами, а отвесные линии в точках 1 и 2 – радиусами этих сфер (рис.2.2), тогда превышение h будет вычисляться по более сложной формуле; приведём вывод этой формулы.
Отметка точки B ’, находящейся на плоскости, отличается от отметки точки B, лежащей на сфере, на величину отрезка BB’, обозначаемого обычно через p (рис.2.1). Из треугольника OCB ’ следует
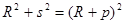 ,
,
откуда получаем
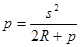 . (2.3)
. (2.3)
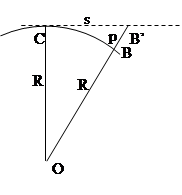 |
Рис. 2.1 – Влияние кривизны Земли на отметки точек
В знаменателе величина p намного меньше величины 2R, поэтому, отбросив ее, мы допустим несущественную ошибку. Таким образом,
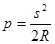 (2.4)
(2.4)
и
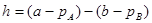 , (2.5)
, (2.5)
где 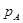 и
и 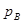 - влияние кривизны Земли в точках А и В соответственно.
- влияние кривизны Земли в точках А и В соответственно.
Влияние кривизны Земли на отметки точек нужно учитывать при любых расстояниях между точками; так, при S = 10 км p = 7.8 м, а при S = 100 м p = 0.8 мм.
Известно, что луч света в атмосфере распространяется по кривой линии, которая называется рефракционной кривой; эту кривую можно считать дугой окружности радиусом 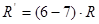 ; отношение радиуса Земли R к радиусу рефракционной кривой R’ называется коэффициентом вертикальной рефракции атмосферы и обозначается через k
; отношение радиуса Земли R к радиусу рефракционной кривой R’ называется коэффициентом вертикальной рефракции атмосферы и обозначается через k
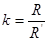 ;
;
численное значение k колеблется от 0,14 до 0,16; в среднем 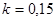 .
.
 Теперь нарисуем полную схему взаимного расположения уровенных поверхностей, отвесных линий и визирного луча при измерении превышения между точками 1 и 2 методом геометрического нивелирования из середины (рис.2.2).
Теперь нарисуем полную схему взаимного расположения уровенных поверхностей, отвесных линий и визирного луча при измерении превышения между точками 1 и 2 методом геометрического нивелирования из середины (рис.2.2).
 |
Рис. 2.2 – Влияние кривизны Земли и рефракции на измеряемое превышение
Превышение точки 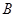 относительно точки
относительно точки 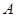 будет равно разности отрезков
будет равно разности отрезков 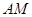 и
и 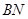
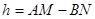 . (2.6)
. (2.6)
Из рисунка видно, что 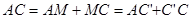 ; обозначим
; обозначим 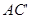 - отсчёт a по задней рейке,
- отсчёт a по задней рейке, 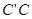 - влияние вертикальной рефракции
- влияние вертикальной рефракции 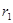 в точке
в точке 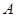 ,
, 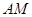 - расстояние между уровенными поверхностями нивелира и точки
- расстояние между уровенными поверхностями нивелира и точки 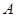 ,
, 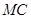 - влияние кривизны Земли
- влияние кривизны Земли 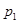 для точки
для точки 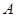 :
: 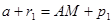 , откуда
, откуда 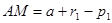 .
.
Из рисунка видно, что 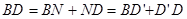 ; обозначим
; обозначим 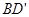 - отсчёт b по передней рейке,
- отсчёт b по передней рейке, 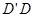 - влияние вертикальной рефракции
- влияние вертикальной рефракции 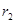 в точке
в точке 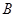 ,
, 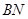 - расстояние между уровенными поверхностями нивелира и точки
- расстояние между уровенными поверхностями нивелира и точки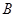 2,
2, 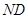 - влияние кривизны Земли
- влияние кривизны Земли 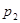 для точки
для точки 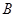 :
: 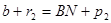 , откуда
, откуда 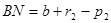 .
.
Далее пишем:
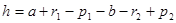 ,
,
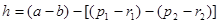 .
.
Величину 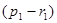 называют совместным влиянием кривизны Земли и рефракции на отсчёт по рейке в точке
называют совместным влиянием кривизны Земли и рефракции на отсчёт по рейке в точке 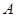 и обозначают
и обозначают 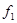 , а величину
, а величину 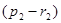 - совместным влиянием кривизны Земли и рефракции в точке
- совместным влиянием кривизны Земли и рефракции в точке 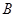 и обозначают
и обозначают 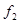 .
.
Далее следуют формулы
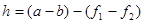 ,
,
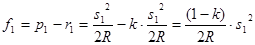 ,
,
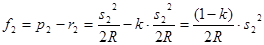 ,
,
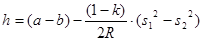 . (2.7)
. (2.7)
Рассчитаем влияние второго слагаемого в последней формуле при 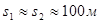 и при
и при 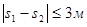 ; получим
; получим
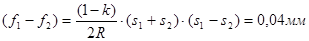 .
.
При 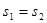 совместное влияние кривизны земли и рефракции становится равным нулю.
совместное влияние кривизны земли и рефракции становится равным нулю.
Вывод: при нивелировании строго из середины влияние кривизны Земли и рефракции на измеряемое превышение почти полностью исключается; остаточное влияние рефракции может иметь место, так как условия прохождения визирного луча до задней рейки и до передней рейки могут отличаться.
ЛЕКЦИЯ 3. УСТРОЙСТВО, ПОВЕРКИ И ИССЛЕДОВАНИЯ ТОЧНЫХ НИВЕЛИРОВ И РЕЕК. МЕТОДИКА НИВЕЛИРОВАНИЯ III КЛАССА; КОНТРОЛИ И ДОПУСКИ.
Устройство, поверки и исследования точных нивелиров
По ГОСТу к точным нивелирам относятся нивелиры, обеспечивающие точность измерения превышений со средней квадратической ошибкой 3 мм на 1 км хода; это нивелиры Н3, Н3К, НВ1 и им подобные.
Государственный стандарт предусматриает следующие основные параметры точных нивелиров:
- увеличение зрительной трубы Vх ³ 30,
- наименьшее расстояние визирования 2 м,
- коэффициент нитяного дальномера 100 ± 1%,
- цена деления простого цилиндрического уровня при трубе 15" ± 1.5",
- цена деления контактного цилиндрического уровня при трубе 30" ± 1.5",
- цена деления круглого установочного уровня 10' ± 2',
- масса не более 3 кг.
Точный нивелир должен обеспечить среднюю квадратическую ошибку измерения превышения на станции не более 2 мм при расстоянии от нивелира до реек 100 м.
Среди точных нивелиров есть нивелиры с уровнем при трубе и нивелиры с компенсатором углов наклона зрительной трубы.
В нивелире с компенсатором визирная линия трубы автоматически устанавливается в горизонтальное положение. Существуют жидкостные, механические и оптико-механические компенсаторы. В настоящее время в нивелирах в основном применяются оптико-механические компенсаторы, в которых главным узлом является подвесное маятниковое устройство. На этом устройстве укреплены оптические детали, предназначенные либо для изменения направления главного визирного луча, проходящего через объектив нивелира, либо для параллельного смещения этого луча. Непременной составной частью оптико-механического компенсатора является демпфер, предназначенный для гашения и ограничения собственных колебаний маятниковых подвесных систем. Приведем схему оптико-механического компенсатора в нивелире Ni-007 (Германия) (рис.3.1).
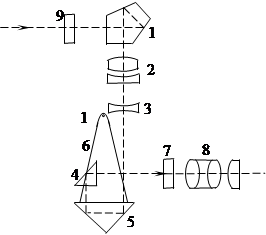 |
Рис.3.1 – Схема оптического компенсатора нивелира Ni-007
На рис.3.1 обозначено: 9 - защитное стекло, 1 - пентапризма для изменения направления горизонтального луча, 2,3 - линзы телеобъектива, 8 – окулярная система призм, 5 – призма маятникового компенсатора, подвешенная на простом физическом маятнике, 4 – неподвижная призма для направления лучей в окуляр 8.
В нивелире Н3К компенсатор состоит из двух прямоугольных стеклянных призм, одна из которых подвешена к верхней части корпуса трубы на двух парах стальных нитей; на рис.12 обозначено: 1 - корпус трубы, 2 - призма, жестко соединенная с корпусом трубы, 3 - призма, подвешенная на нитях, 4 - нити подвеса призмы, 5 - центр тяжести системы,, 6 – демпфер.
С помощью призм изображение рейки передается в плоскость сетки нитей по горизонтальному направлению (S - S) при небольшом наклоне трубы; диапазон компенсируемых углов наклона составляет около 10', ошибка горизонтальности визирной линии трубы - не больше 0,5"; систематическая ошибка недокомпенсации - не более 0,3" на 1' наклона трубы; время затухания колебаний - не более 2 секунд.
Поверки нивелира с уровнем при трубе описаны в [5]; что касается поверок нивелира с компенсатором, то главное условие формулируется несколько по-иному: визирная линия трубы должна быть горизонтальной. Эта поверка выполняется либо двойным нивелированием вперед, либо другим способом [5].
 2014-02-12
2014-02-12 7783
7783








