Основные определения теории графов

История и применение

Глава 3. Введение в теорию графов

Начало теории графов как математической дисциплины было положено Эйлером в его знаменитом рассуждении о кенигсбергских мостах (1736 г.) Однако, она не находила применения в течение почти 100 лет. Интерес к теории возник благодаря исследованиям электрических сетей, моделей кристаллов и структур молекул. В 1847 г. Кирхгофом была разработана теория деревьев, которая послужила важным аналитическим средством для исследования электрических цепей. Законы Кирхгофа для напряжений и токов в цепи полностью определяются контурами и сечениями графа этой цепи и не зависят от природы используемых элементов. Поэтому тщательное изучение понятий контура, сечения и дерева графа дало толчок многим открытиям в теории цепей и, кроме того, внесло большой вклад в теорию графов.

Характерно то, что в терминах графов формулируются многие понятия и задачи прикладных областей: теории игр и программирования, теории передачи сообщений, транспортных сетей, электрических цепей, организационной структуры общества, а также биологии и психологии. В области вычислительной техники теория графов занимает особое место. Она предоставляет большие возможности для построения эффективных алгоритмов и анализа их сложности, дает готовые решения многим задачам вычислительной техники, например, для задачи оптимизации компиляторов. В то же время исследования в каждой из прикладных областей приводят к развитию самой теории графов.

Граф – математический объект, описываемый двумя множествами: G= (V, E), где V – так называемое множество вершин, а E – множество дуг.

Элементами множества дуг являются упорядоченные пары вершин, т.е. E ={ (a, b): a Î V, b Î V }, т.о. множество Е является подмножеством декартова произведения V ´ V. Порядок вершин в парах может и не учитываться, тогда элементы множества Е называют ребрами, а сам граф – неориентированным графом, в противном случае – ориентированным или Орграфом. В некоторых случаях рассматриваются так называемые смешанные графы, в них множество Е состоит из элементов обоих видов: дуг и ребер.

Обозначим вершины v ₁, v ₂, v ₃, ¼, а ребра e ₁, e ₂, e ₃, ¼. Вершины v_i и v_j, определяющие ребро e_k, называются концевыми вершинами ребра e_k =(v_i, v_j), а в случае орграфа – началом и концом дуги e_k соответственно. Говорят также, что ребро e_k (дуга) инцидентно вершинам v_i, v_j или, что вершины v_i, v_j инцидентны ребру (дуге) e_k. Такие вершины называют смежными. Ребра называют смежными в случае, когда они имеют общую концевую вершину. Например, e_k =(v_i, v_j) и e_m =(v_i, v_l) – смежные ребра.

В множестве ребер графа допускается более, чем одно ребро с одинаковыми концевыми вершинами. Такие ребра называются параллельными или кратными. Например: e_k =(v_i, v_j) и e_m =(v_i, v_j) – кратные ребра.

Если обе концевые вершины ребра совпадают, то такое ребро называется петлей. Например: e_k =(v_i, v_i) – петля.

Граф без петель и параллельных ребер называется простым, в противном случае – мультиграфом.

Граф, не имеющий ребер, называется пустым, а не имеющий вершин (а значит и ребер) – нуль‑графом.

Простой граф, у которого любая пара вершин смежна, называется полным.

Количество вершин в графе называется порядком графа.

Степенью или валентностью вершины называется число инцидентных ей ребер. Будем обозначать степень вершины v_i – deg(v_i). Вершина нулевой степени называется изолированной. Вершина степени 1 называется висячей, а ребро, инцидентное ей, называется висячим ребром. Заметим, что петля добавляет двойку к степени вершины.

§ 3.3. Способы задания графов

Рассмотрим три способа задания графов: графический, аналитический и матричный.

1) Графический способ.

Вершины изображают точками на плоскости, а ребра – линиями, соединяющими соответствующие точки. Для изображения дуги используется линия со стрелкой, указывающей направление от начала к концу дуги.

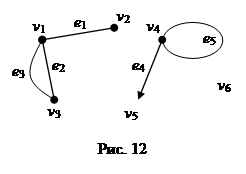На рисунке 12 изображен смешанный граф с вершинами v ₁, v ₂,¼, v ₆, ребрами e ₁, e ₂, e ₃, e ₅ и дугой e ₄. Смежные вершины v ₁, v ₂, инциденты ребру e ₁. Вершины v ₁, v ₃, инциденты параллельным ребрам e ₂ и e ₃. Вершине v ₄ инциденты петля e ₅ и дуга e ₄, причем v ₄ является началом дуги e ₄, а v ₅ – концом этой дуги. Степень вершины v ₁ равна 3, вершины v ₂ – 1, вершины v ₃ – 2, вершины v ₄ – 3, вершины v ₅ – 1, вершины v ₆ – 0. Таким образом, вершины v ₂ и v ₅ – висячие, а вершина v ₆ – изолированная. В случае дуги e ₄ точнее было бы говорить о полустепенях исхода и захода вершин v ₄ и v ₅, а именно: полустепень исхода вершины v ₄ равна 3, вершины v ₅ – 0, полустепень захода вершины v ₄ равна 2, вершины v ₅ – 1.

2) Аналитический способ.

Граф задают перечислением элементов множества вершин и множества ребер. Для графа, изображенного на рисунке 12, эти множества: V ={ v ₁, v ₂, v ₃, v ₄, v ₅, v ₆} и Е ={ e ₁, e ₂, e ₃, e ₄, e ₅}, где e ₁=(v ₁, v ₂), e ₂=(v ₁, v ₃), e ₃=(v ₁, v ₃), e ₄=(v ₄, v ₅), и e ₅=(v ₄, v ₄).

3) Матричный способ.

Имеется несколько вариантов задать граф матрицей. Наиболее употребимыми являются матрица инциденций и матрица смежности.

а) Матрица инциденций – это прямоугольная матрица, число строк которой равно числу вершин, а число столбцов – числу дуг (ребер) графа. Элементы этой матрицы определяются следующим образом:

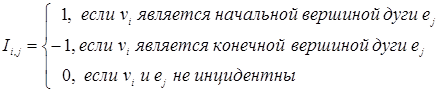
Таким образом, для графа на рисунке 12 матрица инциденций такова:

		e 1	e 2	e 3	e 4	e 5
	v 1
	v 2
I=	v 3
	v 4
	v 5				-1
	v 6

По этой матрице легко судить о наличии в графе параллельных ребер (два одинаковых столбца), петли (одна единица в столбце), дуги (значения разных знаков в столбце), изолированной вершины (нулевая строка), висячих вершин (одно ненулевое значение в строке).

б) Матрица смежности вершин – это квадратная матрица, размер которой определяется числом вершин в графе. Элементы этой матрицы определяются так: 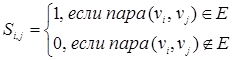. Если в графе имеются параллельные ребра, то соответствующий элемент матрицы смежности полагают равным числу этих ребер. Так матрица смежности для графа на рисунке 12 такова:

		v 1	v 2	v 3	v 4	v 5	v 6
	v 1
	v 2
S=	v 3
	v 4
	v 5
	v 6

По виду этой матрицы также несложно судить о наличии в графе кратных ребер, дуг, петель, висячих и изолированных вершин.

Понятно, что любая квадратная матрица с целыми неотрицательными коэффициентами может быть интерпретирована как граф, а значит, изучение графов можно свести к изучению матриц такого типа. Вообще изучение графов можно расширить, рассматривая матрицы не только с целыми, но и с неотрицательными вещественными элементами. Такие матрицы, например, могут соответствовать графу, представляющему схему дорог, в котором расстояние между вершинами v_i и v_j равно длине соответствующей дороги. Подобные матрицы называют обычно матрицами весов.

Представление графов матрицами очень удобно при решении задач на компьютере.