Подгруппы. Непустое подмножество Н элементов группы G называется подгруппой, если оно само образует группу относительно действия в G

Непустое подмножество Н элементов группы G называется подгруппой, если оно само образует группу относительно действия в G.

Из этого определения следует, что для любых элементов a, b Î H результат действия (a ° b) также принадлежит Н, нейтральный элемент e Î H является также нейтральным и в группе G. И, в силу единственности обратного элемента в группе, ясно, что обратный элемент для любого элемента h из Н будет обратным для h также во всей группе G.

Теорема 2.5.1. (О подгруппе) Непустое подмножество Н группы G является подгруппой тогда и только тогда, когда 1) для любых элементов a, b Î H результат действия (a ° b) также принадлежит Н; и 2) для любого элемента h Î Н обратный элемент h ^–1 также принадлежит Н.

Доказательство. Необходимость следует из определения подгруппы.

Для доказательства достаточности покажем, что нейтральный элемент группы принадлежит подмножеству Н, т.е. е Î Н. Т.к. по пункту 2 для любого элемента а Î Н Þ а ^‑1Î Н, то по пункту 1 результат (а ° а ^‑1)Î Н, но (а ° а ^‑1) = е – нейтральный элемент группы. Таким образом, еÎ Н, что и требовалось доказать. И, следовательно, Н – подгруппа G. (Ассоциативность действия переходит автоматически с G на Н).

Примеры подгрупп:

1) Аддитивная группа четных чисел является подгруппой группы (ℤ, +) целых чисел по сложению, последняя в свою очередь является подгруппой группы (ℚ, +) рациональных чисел по сложению, которая в свою очередь является подгруппой группы (ℝ, +) вещественных чисел по сложению. Все аддитивные группы чисел являются подгруппами группы комплексных чисел по сложению.

2) Мультипликативная группа (ℝ ^>0, ´) положительных вещественных чисел по умножению является подгруппой мультипликативной группы (ℝ \ {0},´) вещественных чисел без нуля и не является подгруппой (ℝ,+), т.к. у них разные нейтральные элементы.

3) Подмножество { e } является подгруппой любой группы. Сама группа также является одной из своих подгрупп.

4) Пересечение любого числа подгрупп группы G является подгруппой группы G.

5) Множество поворотов правильного n ‑угольника вокруг центра на угол 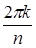, где k =0,1,2,…– является подгруппой группы подстановок S_n и называется группой самосовмещений.