Кольца, тела и поля

Следующими по важности алгебраическими системами являются кольца, тела и поля, которые представляют множества с заданными на них одновременно несколькими действиями. Эти действия, как и в случае групп и полугрупп, могут быть весьма разнообразными. И для обозначения этих действий в общем случае лучше всего было бы употреблять какие–либо отвлеченные от установившихся понятий значки, например: «∘», «*», «j» и т.п.. Однако, по сложившейся традиции, в алгебраических системах с двумя действиями приняты обозначения «+» и «´» (или «×») и при этом используется обычная терминология для этих действий: «сложение» и «умножение». Хотя сами эти действия могут и не иметь ничего общего со сложением и умножением обычных чисел.

Алгебра вида (М, +, ×), которая по «сложению» является абелевой группой, а по «умножению» полугруппой, называется кольцом, если оба действия связаны законом дистрибутивности.

Таким образом, кольцо – это непустое множество, на котором определены действия типа сложения и умножения со свойствами:

а) сложение ассоциативно, обратимо и коммутативно, а также неограниченно применимо на М;

б) умножение неограниченно применимо и ассоциативно на М;

в) оба действия связаны соотношением: для любых x, y и z из М следует (x + y)× z = x × z + y × z и z ×(x + y)= z × x + z × y – двусторонняя дистрибутивность «умножения» относительно «сложения».

Множество М, рассматриваемое по отношению к «сложению», называется аддитивной группой кольца.

Кольцо называется коммутативным, если «умножение» на М коммутативно.

Нейтральный элемент аддитивной группы кольца называется нулем кольца и обозначается 0 _K.

Таким образом, для любого элемента x из М следует: x + 0 _K = 0 _K + x = x и x +(‑ x)= (‑ x)+ x = 0 _K. При этом для каждого элемента x из М и любого натурального числа n определен n ‑кратный элемент nx =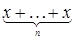, 0‑кратный определяется как 0× x = 0 _K., а обратный к n ‑кратному: ‑(nx)= n (‑ x).

Свойства кольца, связанные с действием «умножения»:

1) Для любого элемента х Î M следует х × 0 _K = 0 _K × х = 0 _K.

Доказательство: действительно, по дистрибутивности х × 0 _K = х ×(0 _K + 0 _K)= х × 0 _K + х × 0 _K. Добавим к левой и правой частям этого равенства обратный элемент: (‑ х × 0 _K). Тогда х × 0 _K +(‑ х × 0 _K)= х × 0 _K + х × 0 _K +(‑ х × 0 _К). В левой части имеем: 0 _К×(х +(‑ x))= 0 _K + 0 _K = 0 _K, в правой части: х × 0 _K + 0 _K ×(х +(‑ x))= х × 0 _K + 0 _K = х × 0 _K. Таким образом, 0 _К = х × 0 _K. Аналогично можно показать, что 0 _K × х = 0 _K.

2) Из предыдущего также следует, что действие «умножения» в кольце необратимо, за исключением лишь случая, когда кольцо состоит из одного лишь элемента 0 _K. Действительно, ни при каком z Î M для х ¹ 0 _K не имеет места ни z × 0 _K = х, ни 0 _K × z = x.

Элементы x, y Î M такие, что х ¹ 0 _K и y ¹ 0 _K и x × y = 0 _K называются делителями нуля. Коммутативное кольцо без делителей нуля называется областью целостности.

Делители нуля в кольце всегда необратимы.

Если кольцо обладает нейтральным элементом по умножению, не совпадающим с нулем кольца, то оно называется кольцом с единицей.

Подмножество I кольца М называется его двусторонним идеалом, если оно само является кольцом относительно действий на М, и если для любого элемента х из М и для любого y Î I следует: x × y Î I и y × x Î I, т.е. правый и левый классы смежности относительно I являются подмножествами I.

Так множество четных чисел является идеалом кольца целых чисел. И вообще множество чисел, кратных любому целому числу k, является идеалом кольца целых чисел.

Примеры:

1) (ℤ, +, ´) – коммутативное кольцо целых чисел, являющееся областью целостности. По сложению – абелева группа, по умножению – абелева полугруппа. Умножение дистрибутивно относительно сложения.

2) Множества ℚ, ℝ, ℂ образуют кольца по сложению и умножению.

3) Множество четных чисел, а также множество целых чисел, кратных произвольному целому числу а: {…, ‑ na,…,‑2 a, ‑ a, 0, a, 2 a,…, na,…} – является коммутативным кольцом относительно обычных действий сложения и умножения.

4) Алгебраические системы (ℕ, +, ´) и (ℚ^>0, +, ´) кольцами не являются.

5) Множество многочленов а ₀+ а ₁ х + а ₂ х ²+¼+ а _n х ⁿ с коэффициентами из некоторого кольца является кольцом относительно почленного сложения и почленного умножения многочленов.

6) Множество классов вычетов по модулю m относительно сложения и умножения классов образует коммутативное кольцо классов вычетов по модулю m и обозначается ℤ _m. Рассмотрим этот пример более подробно.

ℤ _m ={ K ₀, K ₁, ¼, K_{m ‑1}}, где K_i ={ x Îℤ: x mod m = i }, i =0,1,¼, m ‑1. И для любых i и j Î{0,1,¼, m ‑1} сложение классов определяется так: K_i + K_j ={ x + y: x Î K_i, y Î K_j и (x + y) mod m = (i + j) mod m }= K_r, где r = (i + j) mod m. Нейтральным элементом по сложению является класс K ₀, обратным по сложению для любого класса K_i (1 £ i £ m ‑1) является класс K_m‑i, а для класса K ₀ – сам K ₀. Сложение классов коммутативно, ввиду коммутативности сложения целых чисел, и ассоциативно. Таким образом, (ℤ _m, +) – абелева группа. Произведение классов определяется так: K_i × K_j =={ x × y: x Î K_i, y Î K_j и (x × y) mod m = (i × j) mod m }Í K_r, где r = (i × j) mod m. Тем самым умножение классов неограниченно применимо. Коммутативность, ассоциативность и дистрибутивность умножения классов относительно их сложения следует из аналогичных свойств умножения целых чисел. Кроме того, класс K ₁ является нейтральным элементом по умножению классов вычетов по модулю m. Таким образом (ℤ _m, ×) – абелев моноид и (ℤ _m, +, ×) – коммутативное кольцо с единицей.

Рассмотрим кольцо (ℤ₄, +, ×), где ℤ₄={ K ₀, K ₁, K ₂, K ₃ } и K ₀={ x Îℤ: x mod 4=0 }, K ₁={ x Îℤ: x mod 4=1 } и т.д.. Таблицы Кэли для сложения и умножения классов:

+

K 0

K 1

K 2

K 3

×

K 0

K 1

K 2

K 3

K 0

K 0

K 1

K 2

K 3

K 0

K 0

K 0

K 0

K 0

K 1

K 1

K 2

K 3

K 0

K 1

K 0

K 1

K 2

K 3

K 2

K 2

K 3

K 0

K 1

K 2

K 0

K 2

K 0

K 2

K 3

K 3

K 0

K 1

K 2

K 3

K 0

K 3

K 2

K 1

Из таблиц видно, что 0 _К= K ₀, т.к. для любых i =0,1,2,3 K_i + 0 _К= 0 _К+ K_i = K_i и K_i · 0 _К= 0 _К· K_i = K ₀ (первая строка и первый столбец таблицы сложения совпадают с шапкой этой таблицы; первая строка и первый столбец таблицы умножения состоят из одного и того же элемента: K ₀). Коммутативность действий видна из того, что каждая таблица симметрична относительно главной диагонали. Элемент K ₂ является делителем нуля, т.к. K ₂· K ₂= K ₀= 0 _К. Нейтральный элемент по умножению – K ₁, поскольку вторая строка и второй столбец таблицы умножения совпадают с шапкой. У всех элементов, кроме K ₀ и K ₂ имеются обратные по умножению: для K ₁ – сам K ₁, для K ₃ – сам K ₃.

Кольцо с единицей, в котором всякий ненулевой элемент имеет обратный по умножению, называется телом.

Из последнего определения и теоремы о полугруппе ненулевые элементы тела образуют группу, которая называется мультипликативной группой тела. Таким образом, тело объединяет в себе сразу две группы: абелеву аддитивную группу и мультипликативную группу.

Коммутативное кольцо с единицей, в котором любой ненулевой элемент имеет обратный, называется полем. Таким образом, поле – это тело с коммутативным умножением. Аналогичным образом вводится понятие мультипликативной группы поля – это множество ненулевых элементов поля, которые образуют абелеву группу по умножению.

Примеры:

1) ℚ, ℝ, ℂ – образуют поля относительно обычного сложения и умножения. ℤ – поля не образует, т.к. относительно умножения никакие элементы, кроме «+1» и «‑1», не имеют обратных. Но ℤ образует область целостности, т.к. нет делителей нуля, т.е. из равенства a × b =0 следует: либо а =0, либо b =0.

2) Множество квадратных невырожденных матриц фиксированного размера с вещественными элементами относительно операций сложения и умножения матриц образует тело.

3) Кольцо классов вычетов ℤ _p является полем, если p – простое число. Оно называется полем вычетов по модулю p. Легко показать, что у каждого ненулевого элемента имеется обратный. Например, в поле ℤ₇ обратными друг к другу являются элементы: K ₁ и K ₁, K ₂ и K ₄, K ₃ и K ₅, K ₆ и K ₆.

ℤ _p – простейший пример конечного поля. Конечные поля называют полями Галуа и обозначают GF (p). Свойства полей Галуа используются в теории кодирования. Одним из важнейших таких свойств является то, что мультипликативная группа поля Галуа является циклической группой порядка (p ‑1). Порождающий элемент этой группы называется примитивным. Так в поле GF (7) примитивным элементом является класс K ₃. Действительно, K ₃⁰= K ₁, K ₃²= K ₂, K ₃³= K ₆, K ₃⁴= K ₄, K ₃⁵= K ₅, K ₃⁶= K ₁, таким образом, степени элемента K ₃ исчерпывают все ненулевые элементы ℤ₇. Заметим, что класс K ₂ не является примитивным элементом в ℤ₇, т.к. среди его степеней нет, например, класса K ₃. Тогда как в полях GF (3), GF (5), GF (11) и т.д. класс K ₂ – примитивный элемент.